探秘P问题与NP问题:计算复杂度的密码锁
在计算机科学的深邃宇宙里,P问题与NP问题宛如两颗神秘而关键的“双子星”,主宰着我们对计算效率、可解性边界的认知,虽晦涩难懂,却与日常生活、前沿科技紧密交织,暗藏玄机。
P问题:高效解题“快车道”
P问题,是计算机“学霸”能迅速拿捏的“送分题”。简单说,它属于多项式时间可解的范畴,就像有清晰导航的熟路。
比方电商平台按价格排序商品,算法基于预设规则(类似简单排序算法),在数据量(商品数量)增长时,处理时长按多项式函数“温和”增加,
多几件商品无非多几步常规操作,再庞大库存,也能在可预期、可接受时间内完成排序呈现,不耽误你抢购。据谷歌数据,处理百万级商品数据排序,高效算法耗时不过毫秒级,稳且快。
NP问题:棘手“谜题阵”
NP问题则像布满陷阱的迷宫,验证答案易,找答案却似大海捞针。
著名的旅行商问题(TSP)是典型:假设有推销员要跑遍多座城市,求最短回路。给条路线,验证其长度、合法性瞬间能行;
但从零开始穷举所有组合找最优,计算量随城市数飙升,呈指数爆炸!当城市达20个,可能组合超百万亿,超级计算机都得喘粗气,常规算力下,宇宙寿命跑完都未必有结果,复杂度远超P问题“舒适区”。
二者关系:悬而未决的“世纪追问”
P是否等于NP,是学界“圣杯”级悬念。若P = NP,意味着迷宫有秘道,那些曾棘手难题都能被高效攻克,密码破解、物流规划瞬间优化,颠覆金融、安防等诸多领域;
反之,二者不等,则现有计算边界坚固,我们只能在NP难题前用近似法“迂回”。如今,虽倾向P≠NP,但尚未定论。
在科技竞赛场,量子计算崛起给这场“博弈”添变数。理论上,它借量子叠加、纠缠,能对NP问题“弯道超车”。
像分解大整数(NP难),经典计算机望洋兴叹,量子计算机有潜力将时间从亿年缩至数小时,虽实用尚远,却如微光,暗示P与NP“城墙”或有松动之日,激励我们在这抽象却关键的计算疆域持续“拓荒”,解锁更多高效解题智慧。
写在前面
看了很多介绍P与NP概念的文章,但真正讲清楚,并容易理解的文章却是少数。所以本文旨在通俗易懂得讲清楚这些计算复杂性的概念,争取能让非科班出身的小伙伴也能看懂(看不懂请在评论区留下你的疑问)。
本文组织如下:
- 时间复杂度
- P与NP问题
- 多项式时间规约与NP-Complete
- 其他复杂度类
鉴于小伙伴们对这些概念的掌握程度不同,大家可以自行选择感兴趣的章节阅读。
时间复杂度
为什么需要时间复杂度
一个算法,当我们以程序代码,实现在计算机上,有小伙伴可能会吐槽其跑得太慢,或者称赞其跑得很快。这里我们不禁要思考,如何度量一个算法的快慢呢?
运行的物理时间?这恐怕不合适。不同性能的计算机,哪怕是不同的实现语言,都会影响最后的运行时间。
例如同一个task,python可能会比C++慢几十倍[1]
所以我们需要一套更抽象,更数学化的方式来度量一个算法的快慢。更具体得来讲,我们并不希望知道一个算法的具体用时,而是其随输入规模的扩大,用时增长的趋势。于是我们有了时间复杂度的概念。
输入的规模
首先,我们需要明确,所有复杂度讨论的前提是确定输入的规模。
准确的来讲,输入规模等于输入给计算机的比特数。但是这显然太不方便了,没有人会去数到底有多少个0和1。
所以,我们通常会用更直观的方式表示输入规模,例如:
- 数组的大小
- 字符串的长度
- 一个图 G 的节点数量和边的数量
- 多边形的顶点数
- 。。。
不失一般性,我们令输入的规模为 n 。
大 O 符号
在确定了输入的规模之后,要度量算法的快慢,我们面前还有两个问题:
- 不同的输入,哪怕规模一样,同样的算法也可能有不同的运行时间。例如排序,许多排序算法,对一个已经排好序的数组,和一个乱序的数组,也会有不同的运行时间。
- 要准确统计计算机到底执行了多少步加法、乘法等运算,是十分困难的。这也违背了我们将时间复杂度从计算机中剥离出来,成为一个数学概念的初衷。

所以针对第一个问题,我们在度量算法的快慢的时候,需要考虑最坏情况下的输入时的时间复杂度(worst time complexity)。
有时也会考察平均复杂度,但本文讨论的都是最坏情况
而针对第二个问题,我们引入渐进分析来简化分析。所以这里我们使用符号 O ,也就是微积分里面的渐进上界来表示复杂度。这里我们简单讲讲 O 的定义(这个定义看不懂没关系,直接看下面的例子就好):
定义:令 fg 为实数域上两个非 0 的函数。若 \exists x_0 使得当 x\ge x_0 , \exists M\in \mathbb{R}^+ , |f(x)|\le M|g(x)| ,则我们称 f(x)\in O(g(x)) 。
上面的定义比较形式化,通俗点讲, f(x)\in O(g(x)) 可以理解为 f(x) 中增长最快的项,增长速度不会超过 g(x) 中增长最快的项。例如:
2x^3+x^2\in O(x^3) ,这是由于 2x^3+x^2 中增长最快的项为 2x^3 ,而符号 O 允许我们省去常数系数。同样,我们也可以说 2x^3+x^2\in O(x^4) ,因为 x^3 增长速度没有 x^4 快。
除了渐进上界 O ,还有渐进下届 \Omega ,渐进相等 \Theta 。但是本文只讨论渐进上界,是最常用的复杂度度量。
可以看出大 O 符号很好的描述了,一个函数增长的趋势,毕竟我们只关心其增长最快的项。
使用大 O 符号表示时间复杂度
由于大 O 符号允许我们隐去常数项系数与增长相对比较慢的项,所以我们可以简单总结一些规则:
- 加法,减法,大小比较等四则运算,以及赋值,取值,取地址等基本操作都视为一次运算,即 O(1) 。
- 常数次 O(1) 运算,也视为一次运算,即 O(c)=O(1) 。
现在让我们尝试用大 O 符号来表示一些算法的复杂度。
我们考虑一个简单的算法:冒泡排序。
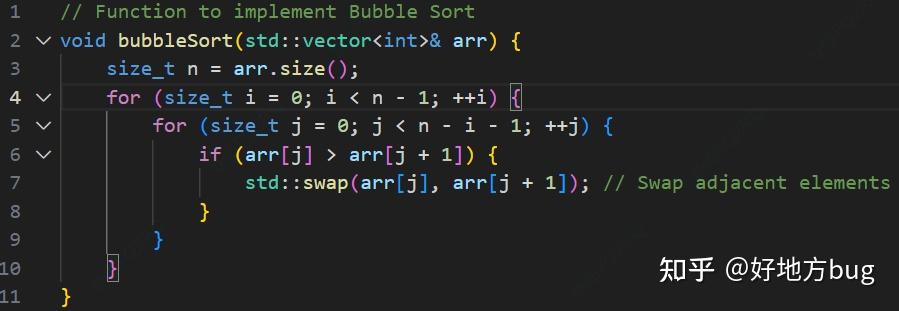
上面的两个规则允许我们不去关心细枝末节的计算开销,所以影响我们算法效率的,显然是第4行与第5行的循环次数。我们来分析一下:
当第4行循环到 i 的时候,第5行需要循环 n-i-1 次。总计我们需要循环的量为求和:
\sum_{i=0}^{n-2}n-i-1=\frac{(n-1)n}{2}=\frac{1}{2}\color{red}{n^2}-\frac{1}{2}n
所以我们的复杂度为 O(\frac{1}{2}(n-1)n) ,而由于我们只用关心增长速度最快的项,且不需要考虑常数系数,所以复杂度可以简单写为 O(n^2) (即上式中红色的那项)。故而我们可以说冒泡排序的时间复杂度 T(n)=O(n^2) 。
我们再考虑一个例子:递归计算斐波那契数列第 n 项。
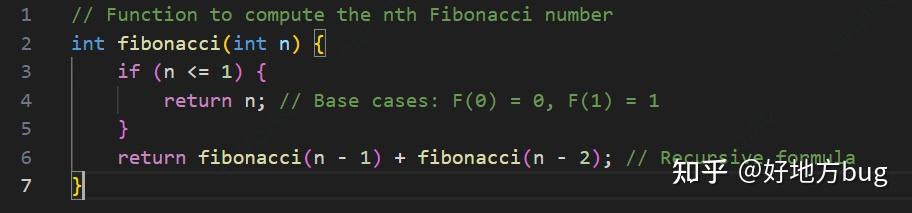
咱知道斐波那契有通项公式效率更高,也知道这样计算容易溢出整型范围。但我们先别考虑这些。
与上面那个冒泡排序不同,这次,我们的算法是递归的,没有显然的循环给我们统计计算量。
我们令 T(n) 为递归计算第 n 项斐波那契数列所需要的时间复杂度。
根据递归的关系(上面代码第6行),计算第 n 项斐波那契数列需要先计算第 n-1 项与第 n-2 项。所以我们有 T(n)=T(n-1)+T(n-2) ,而 T(0)=T(1)=O(1) 。
学过数学分析的同学一定能通过很多办法(特征值法,生成函数法)轻易计算出 T(n) 。我们这里给出一个简单的办法:要计算 T(n) 就需要计算 T(n-1) 与 T(n-2) ,而 T(n-1) 又需要计算 T(n-2) 与 T(n-3) ,如此每一层都成倍增加计算量,如下图所示:
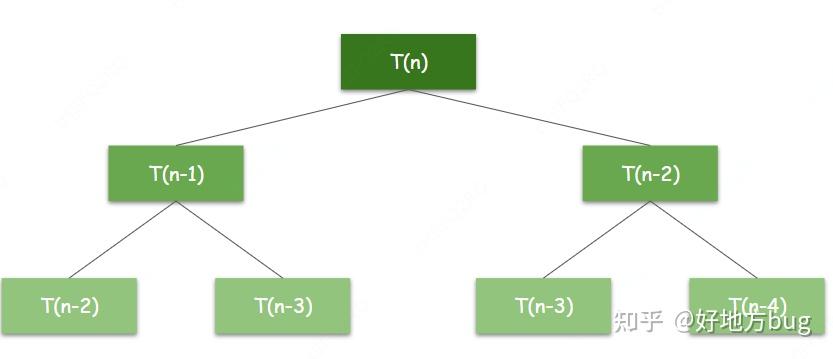
所以我们可以猜到 T(n) 应当是个指数函数。
即 T(n)=x^n 。
代回原式我们有 x^n=x^{n-1}+x^{n-2} ,除以 x^n ,得到 x^2=x+1 。
解一下,得到 x\approx 1.618 (也就是黄金比例)。
综上我们得到,递归计算第 n 项斐波那契数的时间复杂度为 O(1.618^n) 。
下表列举了一些时间复杂度,与为此时间复杂度的常见算法:
| 时间复杂度 | 常见的算法 |
|---|---|
| O(1) | 一次加法运算 |
| O(log n) | 二分搜索 |
| O(\sqrt{n}) | 判断一个数是否为素数 |
| O(n) | 字符串匹配的KMP算法;找到一个数组的最大值 |
| O(nlog n) | 归并排序;凸包算法;单源最短路算法Dijkstra |
| O(n (log n)^2) | Horner's method计算多项式的n个值 |
| O(n^2) | 最长公共子序列 |
| O(n^3) | Floyd求多源最短路 |
| O(2^n * poly(n)) | 用动态规划计算TSP问题,或者图染色问题 |
我们把增长速度低于某个多项式 O(n^k) 的时间复杂度,称为多项式时间复杂度,例如 O(n)O(n\log n)O(n^2)O(n^3) ,这些都是多项式时间。
而对于增长速度低于 O(2^{poly(n)}) 的时间复杂度,称为指数时间复杂度,其中 poly(n) 为 n 的任意多项式。例如 O(n2^n)O(1.0001^n) 都是指数时间复杂度。
下图展示了一些不同复杂度的增长趋势:
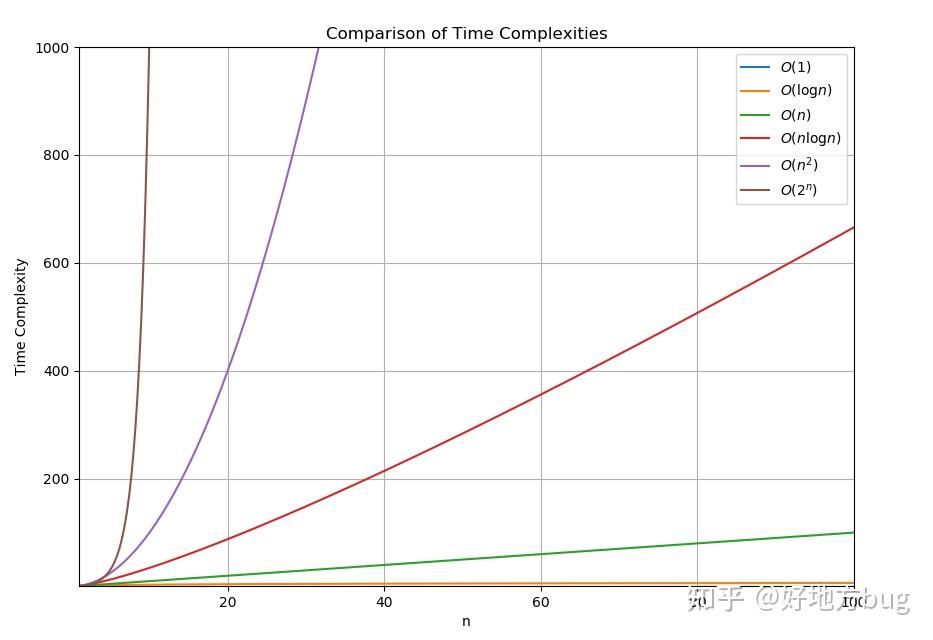
从上面的增长趋势图可以看出,不同复杂度的增长速度有巨大的差别。一般而言,指数级的复杂度,在 n 不断增大的过程中,总是会比多项式级的复杂度增长速度更快。
举个例子,当 n \ge 686 时, 1.1^n > n^{10} 。
P与NP问题
P问题
所以一个问题,如果能在多项式时间内解决,那往往是大家比较喜欢的。毕竟谁也不想CPU跑冒烟了,也得不出结果。所以我们可以对问题进行分类。
注意,接下来我们讨论的问题,都是判定性问题。即,回答yes还是no的问题。这很重要哦,大家记住了。
定义( P ):复杂度类 P 包含所有可以在多项式时间(即 O(n^k) , k 是个常数)内解决的判定性问题。
举一些例子:
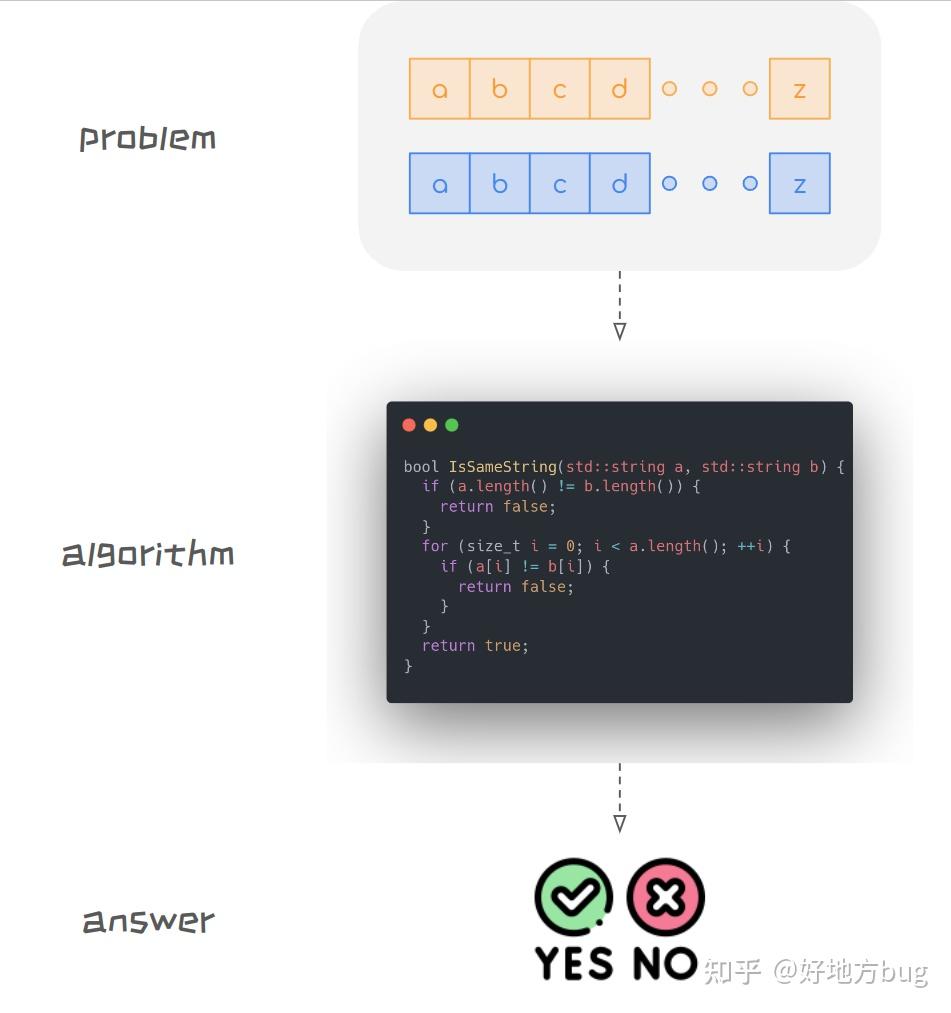
- 给两个长度为 n 的字符串,判断这两个字符串是否相等;
- 给一个 n 个点 m 条边的图 G ,判断其是否连通;
- 给平面 n 个点,判断包围这 n 个点的最小凸多边形,面积是否小于 S 。
对应的算法为:
- 直接 O(n) 时间,挨个比较每一位的字符是否相等;
- O(n+m) 的时间,深度或广度优先搜索,即可判断是否连通;
- O(n\log n) 的时间,可以计算出 n 个点的凸包,从而可以判断面积是否小于 S 。
NP问题
那什么是 NP 问题呢?
很多小伙伴(特别是打比赛的)对 NP 都有所误解。以为NP问题即是没有多项式时间算法的问题,但这是不准确的[2]
这里我们给出 NP 问题的定义
定义( NP ):复杂度类 NP (nondeterministic polynomial time)包含所有判定性问题满足:对于这个问题yes的回答,我们有一个证书(proof),使得我们可以在多项式时间内,通过这个证书,验证这个问题的回答是yes。
有点绕,但是不打紧,我们举些例子:
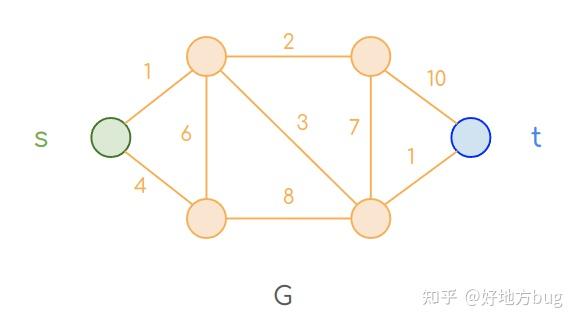
- 最短路问题
- 问题描述:给一个图 G=(V,E) ,边权(都是正数) w:E\rightarrow \mathbb{R}^+ ,一个起点 s ,一个终点 t 。问从起点 s 到终点 t 的距离是否小于L
- 证书:一条长度小于 L 的路线 path ,从 s 到 t 。
- 验证:我只需要验证 path 是否是图 G 中的路线,并且长度小于 L 即可。显然这是可以 O(|path|) 时间内验证的。
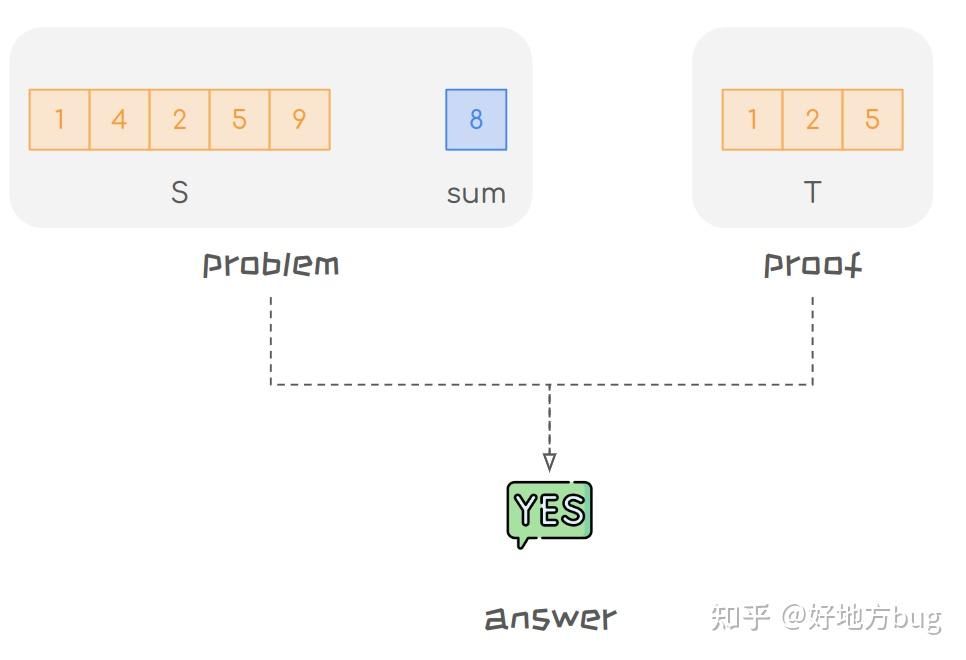
- Subset Sum 问题
- 问题描述:给一个大小为 n 的集合 S\in \mathbb{R}^n ,和一个常数 sum 。问能否找到一个子集 T\subseteq S ,使得 \sum_{t\in T}t=sum 。
- 证书:一个子集 T\subseteq S 。
- 验证:只需要验证 T 的元素的和是否为 sum ,这个的复杂度显然是 O(|T|)\subseteq O(|S|)=O(n) 的。
P=NP or P\ne NP
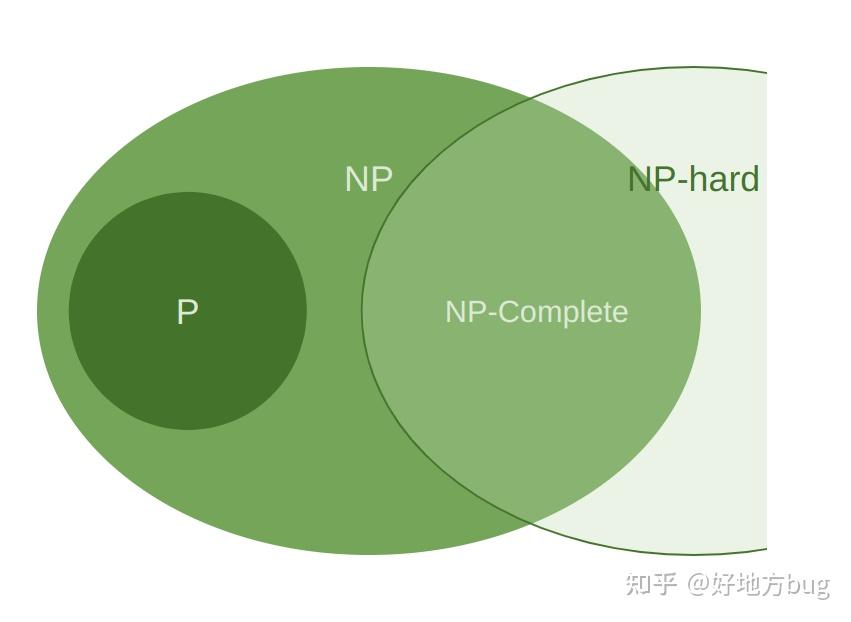
显然一个 P 问题一定是 NP 的,也即 P\subseteq NP 。大家可以停下来想想为啥。
实际上,由于 P 问题,是可以多项式求解的,那么这个求解的过程,本身就是个证书,或者这个问题本身也可以当做是个证书。验证这个证书,所用的时间,自然是多项式的(毕竟求解也是一种验证)。
那反过来呢?
反过来,一个 NP 问题,是否一定是 P 问题呢?或者说,任意一个,我们可以多项式时间验证证书的问题,能否同时找到一个多项式时间的算法求解呢?
这便是著名的千禧难题之一。至今也没有定论。
聪明的小伙伴可以把你对这个问题的答案写在评论区,附带上证明。
多项式时间规约与NP-Complete
多项式时间规约
为了研究这个究极大难题: P=NP or P\ne NP 。我们需要一个工具来研究问题和问题之间的关系。这个工具就是规约。
其实规约很好理解。朴素的来讲,考虑我们有两个问题 A 和 B 。如果任何一个问题 A 的实例(也就是任意问题 A 的输入),都可以转换为问题 B 的一个实例。那只要我们解决了问题 B ,也就解决了问题 A 。那我们就可以说,我们把问题 A 规约到了问题 B 上。
那如果问题 B 是多项式可解的,即问题 B \in P ,并且我们的转换过程是多项式时间可以完成的,那问题 A 自然也就可以多项式可解了,也即 A\in P 。
我们把这种多项式时间的规约记为符号 \preceq_p 。在上面这个例子中,即 A\preceq_p B 。
这个符号非常形象,看着像是小于等于,其实对应的即是,在多项式时间的意义下,问题 A 没有问题 B 难。
举个例子
我们还是考虑上面最短路问题(SHORTEST PATH PROBLEM)的例子。
定义(最短路问题):给一个图 G=(V,E) ,边权(都是正数) w:E\rightarrow \mathbb{R}^+ ,一个起点 s ,一个终点 t,和一个常数 L 。最短路问题(SHORTEST PATH PROBLEM)问从起点 s 到终点 t 的距离是否小于L 。
我们把最短路问题规约到线性规划问题(为了方便,我们这里不使用判定性问题的形式表达线性规划问题)上。
定义(线性规划标准型):给定向量 c ,矩阵 A ,向量 b 。线性规划(LP)求:
- 寻找向量 x
- 最小(大)化 c^Tx
- 满足 Ax\le b
- 且满足 x\ge 0
要用线性规划解决最短路问题并不困难,我们只需要寻找一个向量 d ,其中 d(u) 表示从起点 s 到 u 的最短路的长度。那么只要找到了这个 d ,通过验证 d(t) 是否小于 L ,即可回答最短路问题。我们这么来构造这个线性规划:
对于任意一条边 (u,v) 而言,我们到达点 v ,可以选择
- 先从起点 s 走某个路线到 u ,再走 (u,v) 到 v ;
- 或者不走 (u,v) ,直接从起点 s 出发,由别的路线到 v 。
即有 d(v)\le d(u)+w(u,v) 。
所以表达成线性规划即是:
- 寻找向量 d
- 最小化 d(t)
- 满足, \forall (u,v)\in Ed(v)\le d(u)+w(u,v)
- 且满足 d(s)=0d(u)\ge 0\forall u\in V
上面这个线性规划离标准型还有一点点距离,只需要稍稍转换即可,这里省略
我们的转换过程显然是多项式时间可以完成的。故而我们可以说我们在多项式时间下将最短路问题规约到了线性规划问题:\text{SHORTEST PATH PROBLEM} \preceq_p \text{LP} 。也即最短路问题在多项式时间意义下没有线性规划问题难。
由于 \text{LP} \in P ,所以 \text{SHORTEST PATH PROBLEM} \in P 。即最短路问题是可以多项式时间可解的。
NP-Complete
嗯,很好,我们通过规约证明了最短路问题是多项式可解的,那对于其他的NP问题呢?
为此,我们需要先了解一个非常关键的NP问题:SAT问题。
学过离散数学或者数理逻辑的小伙伴应该有更详细准确的定义,这里我们抛掉与本文无关的概念,尽量简单定义这个问题
我们令 \wedge 为且运算(即C++中的&&),令 \vee 为或运算(即C++中的||),令 \neg 为取反运算(即C++中的!)。
考虑若干布尔变量 x_1,x_2,\cdots,x_n 。一个子句为其中一些布尔变量,或者其取反后的布尔变量的或运算。例如 x_1\vee x_4 \vee \neg x_7 ,或者 \neg x_2\vee x_3 都是子句。
定义(SAT问题):给定一组布尔变量 x_1,x_2,\cdots,x_n 。和若干子句 C_1C_2,\cdots,C_m 。是否存在一种 x_1,x_2,\cdots,x_n 的取值,使得 C_1\wedge C_2\wedge \cdots\wedge C_m = \text {True} 。
在1971年时,Cook证明了所有 NP 问题都可以规约到 \text{SAT} 问题上。即 \forall \text{PROBLEM}\in NP\text{PROBLEM} \preceq_p \text{SAT} 。
所以我们称 \text{SAT} 为NP完全(NP-Complete)问题。即任何 NP 问题都没有 NP 完全问题难(多项式时间意义下)。
证明省略[3]。
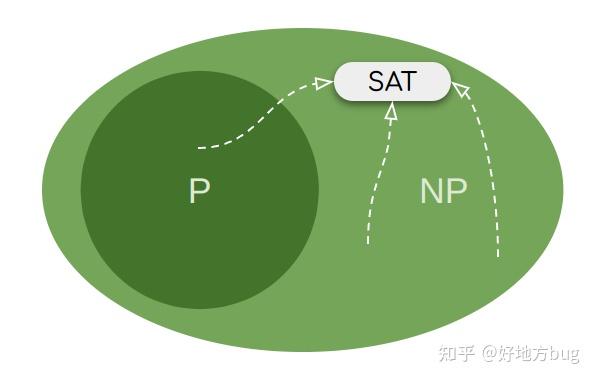
换句话说,我们只要证明了 \text{SAT} 问题是多项式可解的,那么所有 NP 问题都将多项式可解。
当然现在还没有被承认的证明
那只有一个 \text{SAT} 问题,未免使得 NP 完全问题太过单调。如果 \text{SAT} 问题能够规约到别的 NP 问题上,那就能把别的问题也加入 NP 完全的家族。
我们这里再介绍两个NP完全家族的成员。
从SAT规约到3-SAT
3-SAT问题和SAT问题类似,唯一区别在于每个子句恰好包含3个变量。
定义(3-SAT问题):给定一组布尔变量 x_1,x_2,\cdots,x_n 。和若干子句 C_1C_2,\cdots,C_m ,且每个子句恰好包含3个变量。是否存在一种 x_1,x_2,\cdots,x_n 的取值,使得 C_1\wedge C_2\wedge \cdots\wedge C_m = \text {True} 。
规约:
对于每个 \text{SAT} 问题的实例,我们考虑其任意一个子句 l_1\vee l_2\vee\cdots\vee l_n ,我们可以通过引入一系列新的变量,将其转换为:
(l_1\vee l_2\vee x_2)\wedge\\(\neg x_2\vee l_3 \vee x_3)\wedge\\ (\neg x_3\vee l_4 \vee x_4)\wedge \cdots \wedge \\ (\neg x_{n-3}\vee l_{n-2} \vee x_{n-2})\wedge\\ (\neg x_{n-2}\vee l_{n-1} \vee l_n)\\这和原子句等价。而且虽然转换出来的这一系列新的子句很长,但显然也是多项式级别的。故而我们的规约是可以在多项式时间完成的。
也即 \text{SAT} \preceq_p \text{3-SAT} 。
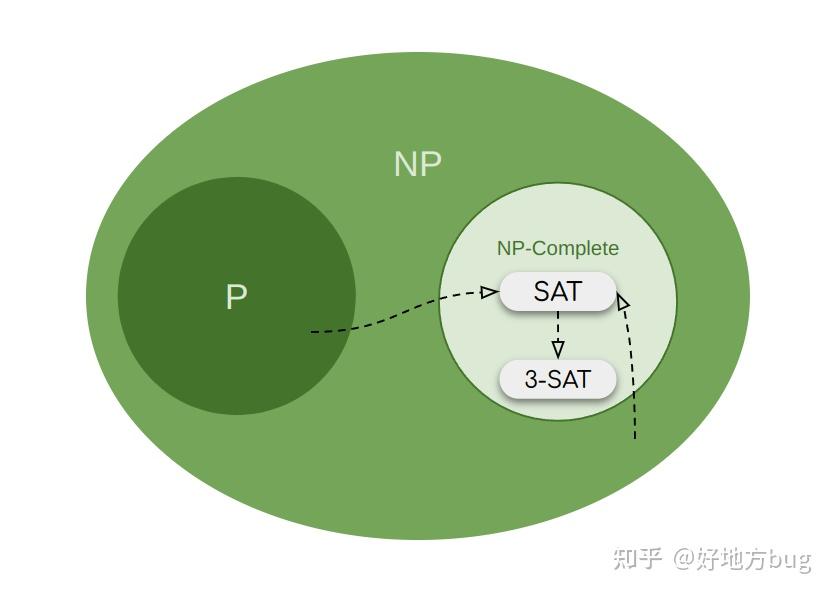
从3-SAT规约到独立集问题
不管怎么说3-SAT始终还是SAT的表亲,它是NP完全的,情有可原。那我们现在来证明一个八竿子打不着的图论问题,也是NP完全的。
定义(独立集问题):给定一个图 G=(V,E) ,独立集问题( \text{INDEPENDENT SET} )问是否存在一个大小为 k 的点子集 S\subseteq V ,使得 S 中的点两两不连接,即 \forall u,v\in S(u,v)\notin E 。
规约:
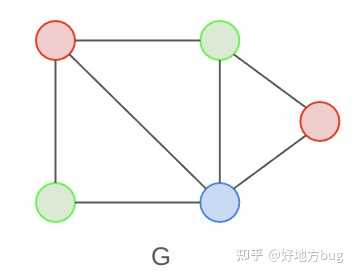
考虑任意一个 \text{3-SAT} 的实例 \phi ( n 个变量, m 个子句),我们构造一个图 G 。对于每个子句 C_i 的三个变量 l_{i,1}l_{i,2}l_{i,3} ,我们构造三个顶点 v_{i,1}v_{i,2}v_{i,3} 。并且将这三个顶点两两连接。
接下来,对于任意的两个顶点,如果其对应的变量是相互取反的关系(例如 x 和 \neg x ),则在这两个顶点间连接一条边。
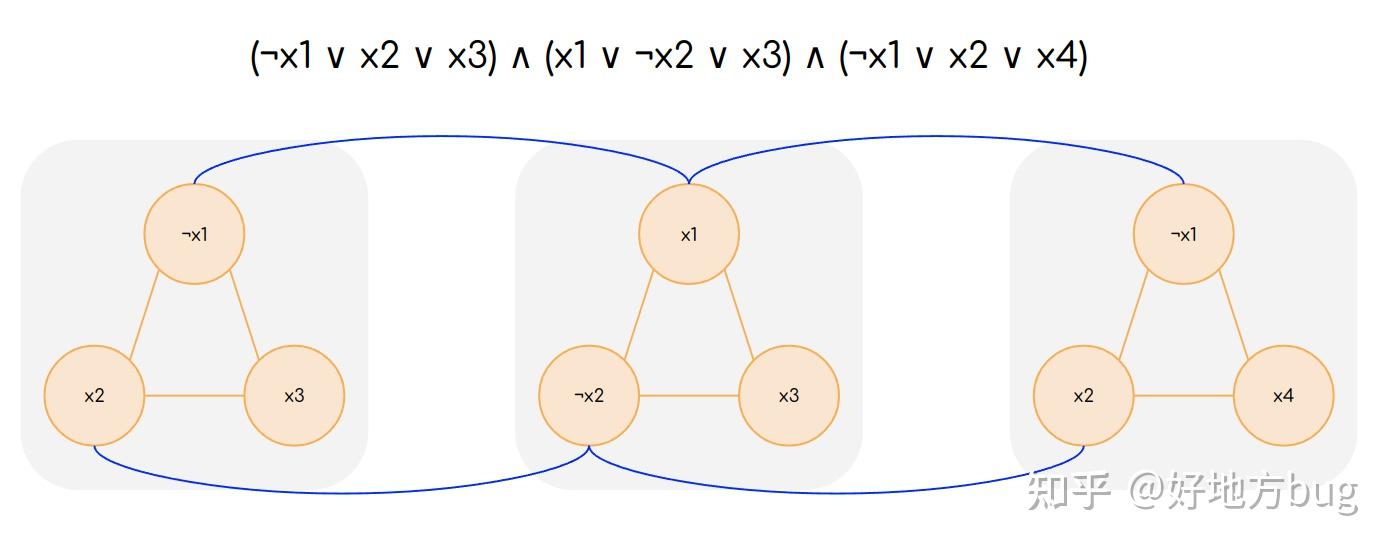
这时,我们可以断言, \phi 可以取 \text{True} 当且仅当 G 中存在一个大小为 m 的独立集。
证明:
\Rightarrow :
当 \phi 取 \text{True} 时,那么每个子句至少有一个变量取 \text{True} 。所以我们对于每个子句,任取一个其为 \text{True} 的变量对应的节点,加入集合 S 。最后集合 S 一定是独立集,且 |S|=m 。这是由于首先每个子句我们只取了一个,所以每个子句内对应的边都不会连接 S 中的不同顶点。其次,由于每个变量和其取反的变量不可能同时取 \text{True} ,故连接相反变量之间的边,也不会连接 S 中的不同顶点。而 |S|=m 则是显然的。
\Leftarrow :
当 G 有大小为 m 的独立集 S 时。 必然每个子句对应的三个节点,刚好有一个在 S 中(否则根据鸽笼原理,若一个子句对应的三个节点都不在 S 中,则一定有某个另外的子句,至少有两个点在 S 中,这与 S 是独立集矛盾)。而由于 G 的构造保证相反的变量对应的节点是相连的,即 S 中不会同时出现 x 与 \neg x 。所以 S 对应的变量若都取 \text{True} ,则 \phi 取 \text{True} 且是个合法的取值。
QED
通过这个构造型的证明,我们说明了,通过独立集问题,我们即可解决 \text{3-SAT} 问题。即有:
\text{3-SAT}\preceq_p\text{INDEPENDENT SET}
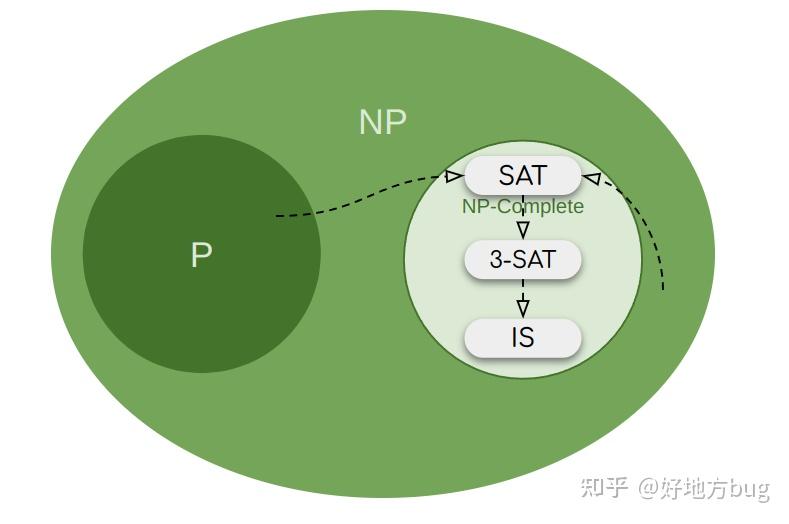
其他NP-Complete问题
NP-Complete问题其实非常非常多,例如
- 背包问题
- 划分问题
- 子集和问题
- 旅行商问题
- 图染色问题
- 点覆盖问题
- 等等等等[4]
下图展示了常见的NP-Complete问题之间的规约关系[5]
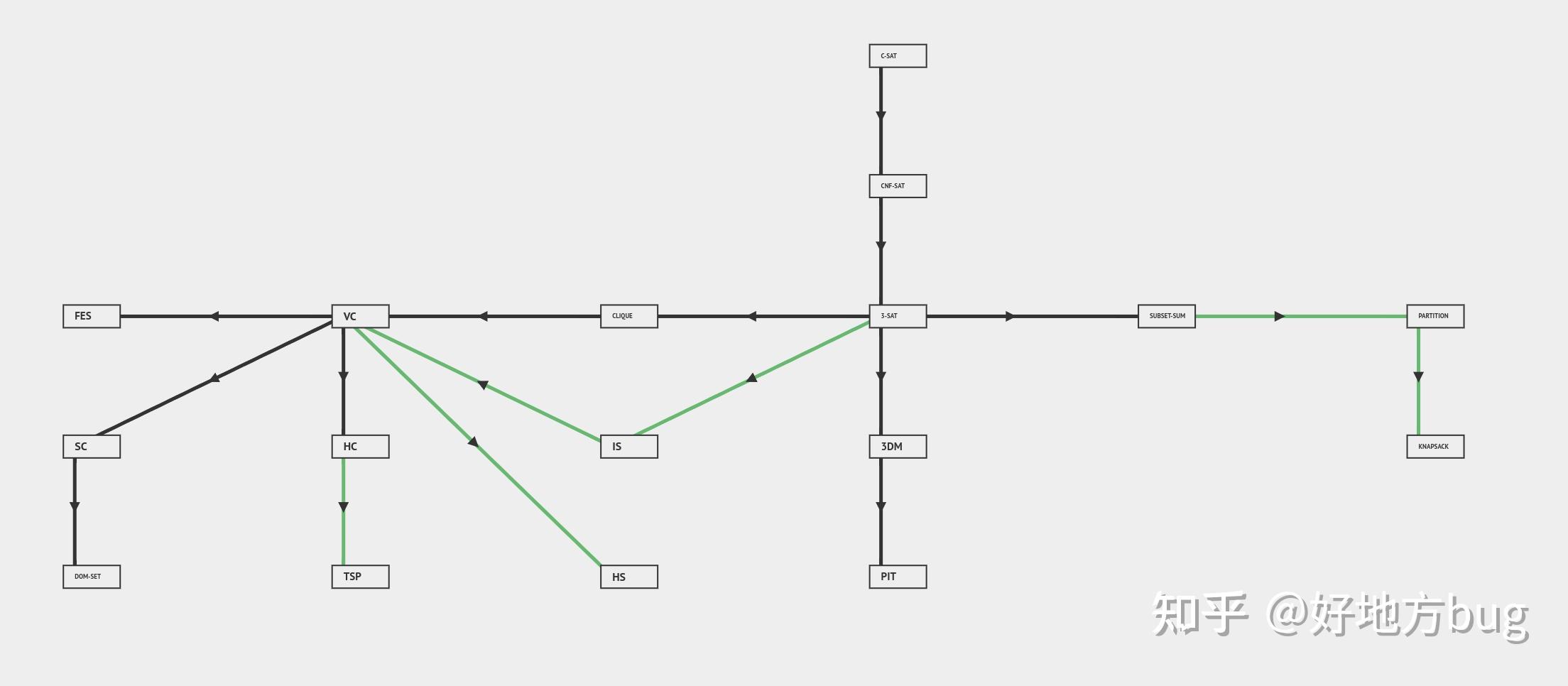
其他复杂度类
NP-hard
这个最容易理解,在多项式时间意义下,不比NP-Complete更简单的问题。
PSPACE与PSPACE-Complete
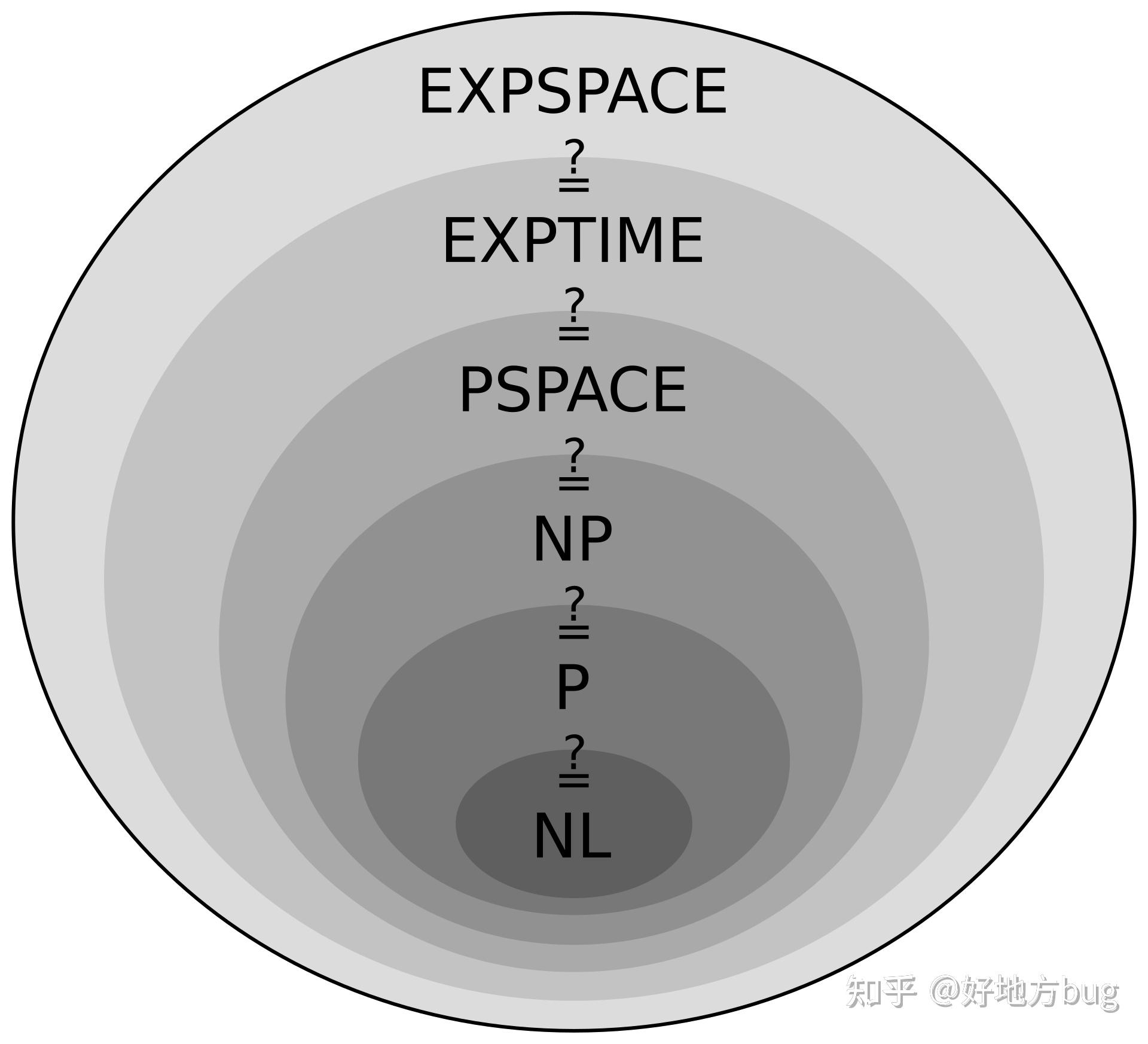
PSPACE:只用多项式空间的算法就能解决的问题。
PSPACE-Complete:即PSPACE中,不比任何其余PSPACE问题更简单的问题(类似NP-Complete)。一般一些计数问题在此列。
EXPTIME
即,指数时间内能解决的问题。
写在后面
其实除开这些,计算复杂性理论还有非常多非常多精彩的内容。无数的科研工作者,将成百上千个问题的求解边界(包括上界和下界)都做了详细的讨论。这不是这篇科普文章能够展开的。如果大家有兴趣,可以去阅读相关书籍和论文。
另外,随着量子计算机的兴起,复杂度类的种类又被扩充了一圈,即在量子计算机上的可求解性。
至于NP到底等于不等于P,我个人认为是不等的(虽然也看过不少证明他们相等的论文,我也没找出什么bug),静待时间(大牛,或者阅读到这里的你)来告诉我们答案。
最后,好长啊,我第一次写这么长的文章。
求点赞!关注!收藏!
参考
- ^https://www.freecodecamp.org/news/python-vs-c-plus-plus-time-complexity-analysis/
- ^http://www.matrix67.com/blog/archives/105
- ^https://en.wikipedia.org/wiki/Cook%E2%80%93Levin_theorem
- ^https://en.wikipedia.org/wiki/List_of_NP-complete_problems
- ^https://visualgo.net/en/reductions