6.1　配合物的稳定性

6.1　配合物的稳定性

配合物的稳定性包含配合物在溶液中的配位稳定性和氧化还原稳定性等。在溶液中的配位稳定性是指配离子在溶液中解离成金属离子和配体，当解离达到平衡时解离程度的大小。氧化还原稳定性是指配合物中金属离子得失电子的难易程度。

6.1.1　配合物的稳定常数及测定

作为 Lewis 酸碱加合物的配离子或配合物分子，在水溶液中存在着配合物的解离反应和生成反应之间的平衡，这种平衡称为配位平衡[1] 。如将氨水加到 CuSO4 溶液里，会有 [Cu(NH3)4]2+ 生成，当生成反应和解离反应速率相等时，体系达到平衡状态，反应式如下：

Cu2+ + 4NH3 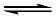加载中...[Cu(NH3)4]2+

由化学平衡原理，可得到

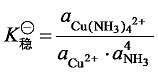加载中...　　(6-1)

式中，a表示各质点的平衡活度。这个平衡常数称为 [Cu(NH3)4]2+ 的热力学稳定常数 （或生成常数），此常数越大，说明生成配离子的倾向越大，而解离倾向越小，即配离子越稳定。由此可见，稳定常数 （stability constants） 是衡量配合物稳定性大小的尺度。

对于一般的配位平衡，可用下列关系式表示 （为简便起见，略去电荷）：

n M +l L +p P + h H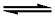加载中...MmLlPpHh

式中，M、L、P、H 分别代表金属离子、第一配体、第二配体、氢离子；m、l、p、h 分别代表相应物种在形成配合物时的计量系数。这样形成配合物 MmLlPpHh 的热力学稳定常数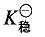加载中...可表示为：

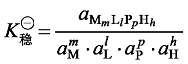加载中...　　(6-2)

式中，a表示各质点的平衡活度。当h 为 0 时，表示在配合物中没有氢离子；当h 为负整数时，表示在形成配合物时失去氢离子或加上氢氧根离子。

自由的金属离子在溶液中非常罕见，金属离子周围通常都有溶剂分子，它们将与配体发生竞争作用而逐步被配体取代，实际上这种取代反应是分步进行的，在溶液中有各级配离子存在。如在含 Ag+ 的溶液中加入氨水，则二氨合银配离子可按下面两个步骤生成：

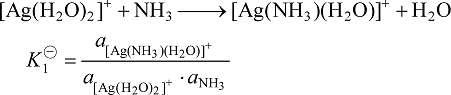加载中...　　(6-3)

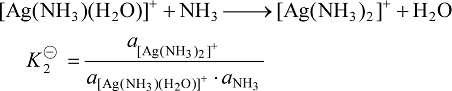加载中...　　(6-4)

其中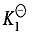，加载中...和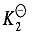加载中...称为逐级稳定常数 （或逐级生成常数）。很容易证明，逐级稳定常数的乘积就是该配离子的总稳定常数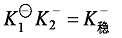：加载中...。

配离子的逐级稳定常数一般差别不大，除少数例外，常是比较均匀地逐级减小，即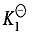加载中...>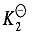加载中...>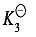加载中...>…>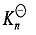加载中...，这是因为后面配位的配体受到前面已经配位的配体排斥之故。特别是配体带有电荷时斥力更大，逐级稳定常数的差别也更大。

稳定常数数据的积累可以为配合物的形成、结构以及中心原子和配体间成键的本质等方面提供有用的资料。在实际应用方面，如离子交换、溶剂萃取和螯合滴定等均以配合物在溶液中的稳定性为基础。配合物在溶液中形成时，常引起某一种物理量的改变。测定稳定常数的方法就是以此为基础。配合物稳定常数的测定已研究了半个多世纪，提出了很多方法[2] ，大致有以下几种：

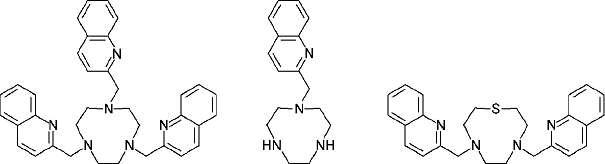
(1)电位法　以研究溶液中离子与电极的相互作用为基础，测定金属离子或配体的活度。电位法所测的数据精确，适用于单核和多核配合物的研究，应用范围最广泛。用电位法测定稳定常数时，要求电极反应必须是可逆的。使用的电极主要有金属或金属汞齐电极、氧化还原电极和离子选择性电极三种。金属汞齐电极使用较广，适用于 Cu2+、Zn2+、Cd2+、In3+、Tl+、Sn2+、Pb2+、Bi3+ 等金属配合物的研究。通过测量溶液的实际 pH 变化，并由此计算配体的平衡浓度，则称为 pH 电位法。早期提出的主要是由 Bjerrum 生成函数 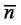加载中... 引申出来的半整数法和罗索蒂 （Rossotti） 所改进的图解法。这两种方法主要针对的是单核、单配体的体系。随着计算机科学的发展，采用了最小二乘法、HOSK 法等数据处理方法。2009 年，V. Lippolis 等[3] 报道了下列 3 个带臂大环配体 （图 6-1） 对 Zn2+ 的荧光识别研究，文中作者用电位法测定了配合物的稳定常数。

加载中...

图 6-1　V. Lippolis 等人报道的带臂大环配体的结构式

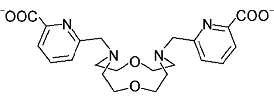
2009 年，C. Platas-Iglesias 等[4] 报道了以 pH 电位法测定了带臂大环配体 [bp12c4]2– （图 6-2） 与稀土 Gd3+ 形成的配合物的稳定常数。

加载中...

图 6-2　C. Platas-Iglesias 等报道的配体 [bp12c4]2– 的结构式

(2)极谱法　也是一种以研究溶液中离子与电极的相互作用为基础的方法。根据加入配体后金属离子的半波电位的改变来计算稳定常数，在金属离子可逆还原条件下，能得到单核配合物和混合配合物的稳定常数。该法数据准确可靠，灵敏度高，特别适用于浓度和稳定性较低的配合物。对某些不可逆还原的金属离子，可采用竞争法或利用扩散电流随配体浓度改变的关系来计算。

(3)分光光度法　当配合物的吸收光谱与金属离子有所不同，且溶液在某一波长的光密度与组成的关系符合比尔定律时，稳定常数可通过计算求得。其优点是迅速可靠，适用于低浓度 (10–5~10–4 mol·L–1) 的配合物，溶剂选择的范围比电位法广，但处理数据的未知数比电位法多，对较复杂体系的计算有一定困难。

(4)萃取法和离子交换法　均以金属配合物的异相分配为基础，通过测定分配比来测定稳定常数。这两种方法的精确度不如电位法，但不低于分光光度法，特别是当金属离子浓度很低时，可采用放射性手段来测定，这是其独特的优点。萃取法适用于研究螯合物，不适用于稳定性较低的配合物。离子交换法适用于微量的或含放射性金属离子的配合物的研究，但步骤较烦琐，数据不够精确。

(5)量热滴定法　又称测温滴定法，是 20 世纪 60 年代发展起来的一种新方法，根据配位反应的热效应来确定组成和稳定常数。该法用热敏电阻感温，用计算机计算，通过一次滴定可同时求得配位反应的焓变 (ΔH) 和稳定常数值，能直接而准确地获得 ΔH、吉布斯函数变 (ΔG) 和熵变 (ΔS) 值。此法应用范围广，反应条件适应性强，对高酸性、高碱性和非水体系均可适用，特别适用于 pH 值恒定的生物缓冲体系；但不如 pH 电位法和分光光度法有高度的专一性。因其计算复杂，校正项多，用于复杂体系时有一定的困难。

2009 年，R. van Eldik 等[5] 报道了 Fe(Ⅲ) 与 cydta [（±）-反-1,2-环己二胺四乙酸]　形成的配合物的晶体结构，并用量热滴定法测定了配合物的稳定常数，热力学研究表明该配合物比 Fe(Ⅲ) 与 edta （乙二胺四乙酸） 形成的配合物具有更高的稳定性。

(6)其它方法　均以配位过程中某一物理量的改变为基础，如核磁共振法以化学位移或偶合常数为基础，顺磁共振法除根据偶合常数外，还可根据谱线宽度 （弛豫时间）、谱线强度 （自旋浓度） 及朗德因子 (g) 值来计算。这些方法皆有局限性，使用范围不广。

6.1.2 配合物的氧化还原稳定性

金属离子在水溶液中形成配合物的氧化还原稳定性与配合物的组成、结构等因素有关，配合物之间的氧化还原反应是指电子从一个配合物分子的中心原子转移到另一个配合物的中心原子上。

当体系中加入某种配体使金属离子形成配合物后，溶液中金属离子的浓度降低，该电对的电极电势值也降低，即配合物的生成改变了金属离子氧化态的氧化能力和还原态的还原能力[6] 。例如，电对 Co3+/Co2+的标准电极电势为 1.92 V，在热力学标准态下，Co3+ 能将 H2O 氧化放出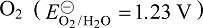加载中...，是很强的氧化剂，所以不能在水溶液中制备三价钴盐。如在 Co3+中加入氨水生成稳定配合物后，则电极反应为：

[Co(NH3)6]3+ + e 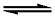加载中... [Co(NH3)6]2+

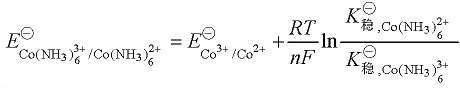加载中...　　(6-5)

由此可计算出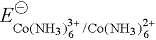加载中...为 0.18 V，于是 Co[(NH3)6]3+ 能够在水溶液中稳定存在。

推广到一般，假设有某变价金属离子 Mm+与 Mn+，分别与同一配体形成配位数相同的配合物，稳定常数分别为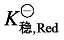加载中...和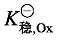加载中...，溶液中离子在电极上发生的反应为：

Mn+ + (n–m) e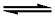加载中...Mm+

MLxn+ + (n–m) e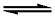加载中...MLxm+

则配离子电对的电极电势为：

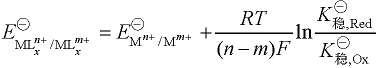加载中...　　(6-6)

式中，m、n为正整数，且n >m；x为配体 L 的数目。依据此公式可计算出金属离子形成配合物后，其配离子间电对的标准电极电势值。

当一个电对的氧化型和还原型同时生成配合物后，对中心原子的氧化还原稳定性会产生一定影响。下面分别进行讨论：

(1) 配合物的形成稳定了高价态的金属离子　从式(6-6) 可以看出，若 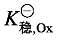加载中...>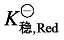加载中...，则配离子电对电极电势与金属离子电对相比降低，金属离子高价态稳定。这是由于同一金属不同价态离子的配合物稳定性不同 (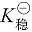加载中...不同)，使溶液中游离金属离子浓度发生变化，从而引起电极电势的改变。如 Co3+ 在水溶液中因有较强的氧化性而不能稳定存在，但当 Co3+ 形成配合物后则不容易被还原了。