§2.6 平衡的稳定性与运动的稳定性
§2.6 平衡的稳定性与运动的稳定性
从上一节的分析看到，当我们不满足于 Lagrange 力学古典研究的成果，考虑到为了求解动力学问题并使解便于在技术上使用而发展某些近似方法的时候，稳定性问题必须首先加以研究.由 Lagrange 开始，并由 Poincaré 和 Ляпунов 所发展的稳定性理论开创了动力学问题定性研究的方向.稳定性研究的成果本身就有重要的实际意义，同时也给某些近似方法提供了依据.
2.6.1 平衡位置的稳定性
首先研究力学系统平衡位置的稳定性.考虑一个完整的力学系统，其广义坐标为 q1，q2，…，qn，现在我们所说的平衡位置是对广义坐标空间来说的，它的含义是：如果系统在 t=t0的初始状态为
加载中...通过简单的平移变换，可以使平衡位置变到广义坐标空间的原点.因此，不失一般性，可以认为我们讨论的平衡位置就是
加载中...这样，系统运动时的广义坐标 q1，q2，…，qn刚好代表了系统离开平衡位置的偏差.
既然假定坐标原点是系统的平衡位置，因此，q1=q2=…=qn=0 从数学上来说，一定是动力学方程的一个解案.但是，这个解案能不能在实际中真正实现呢？一般地说，对动力学方程任何一个解案都可以提出这样的问题.回答这个问题就必须考虑这个解案的稳定性.仅就平衡位置的稳定性而论，这个稳定性概念可以严格定义如下：
定义 任给一个 ε>0，不管它是如何地小，我们总可以找到一个相应的 η>0，使得，只要扰动引起的初始状态和平衡状态之间的偏差满足
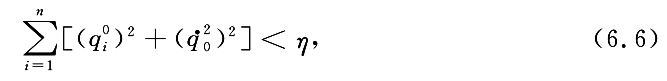加载中...就有
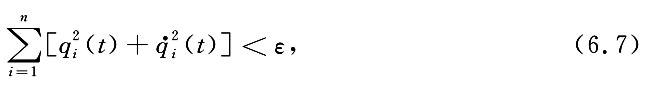加载中...其中 t≥t0.具有这样性质的平衡位置 q1=q0=…=qn=0 称之为稳定的平衡位置.反之，不具有上述性质的平衡位置称之为不稳定的平衡位置.
可以在状态空间 Sq里很直观地来理解上述定义的几何含义：为了使系统实际运动的状态点永远离开平衡状态点 s0不远（例如，限制在以 s0为球心、任给的 ε>0 为半径的球内），只要限制初始扰动状态离开平衡状态不远（例如，限制初始状态位于以 s0为球心、以相应的 η>0 为半径的球内）就能达到.这就是稳定平衡位置的性质.反之，对于不稳定的平衡位置，它的性质就是：对于任给的 ε0>0，无论它是多么的小，总可以找到某个 0＜ε＜ε0，使得对于这个 ε 球面而言，无论上述的 η 多么的小，总至少可以找到一条 s 轨迹，它在 t=t0从 η 球内出发，而后却跑到 ε 球面以外.
对于判别平衡位置的稳定性，如果我们已经找到了系统的通解，那么利用通解来分析稳定性当然是一种可能的途径.但是在大部分问题中，上述通解是不知道的.因此，更为实际的方法是在不知道通解的情况下寻找稳定性问题的解法.以下定理给出了保守系统平衡位置及稳定性的判别准则.
加载中...根据条件（6.4），这就证明了 q1=q2=…=qn=0 为平衡位置.以下证明它是稳定的.
考虑系统的机械能函数
加载中...
加载中...在这个球面上，每个点的 E 函数值都是大于零的，即有下界.由于这个球面是一个闭域，因此函数 E 在球面上有下确界.记此下确界为 Emin.由于这个 Emin在 ε 球面上一定能取到，所以有
Emin>0. （6.15）
由于 E 函数是状态变量的连续函数，而 E｜s0=0，因此，一定可以找到 δ>0，只要
加载中...就有 E 函数的值小于 Emin.
根据保守系统的机械能守恒规律，有
dE/dt=0， （6.17）
积分之，得到
E=h=const.. （6.18）
加载中...2.6.2 运动稳定性的一般概念
考虑一个理想、完整的力学系统，其广义坐标为 q1，q2，…，qm，它的动力学方程由第二类 Lagrange 方程显式（3.15）给出：
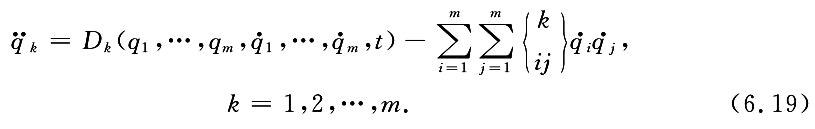加载中...引入系统的状态空间 Sq的变量
加载中...那么由（6.19）式立即得到系统状态变量的动力学方程为
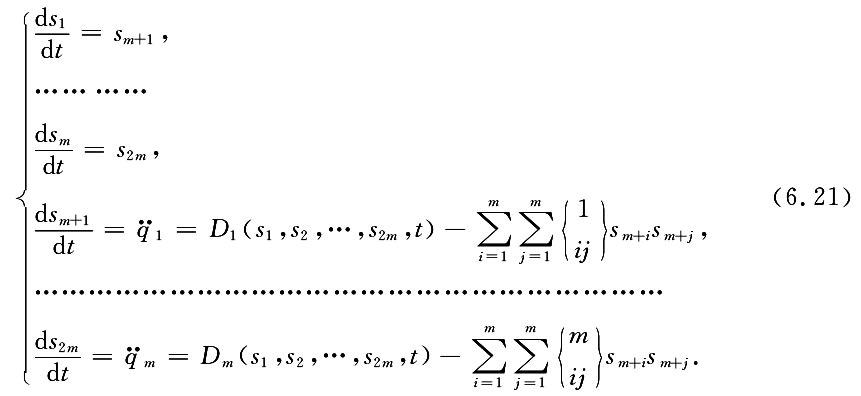加载中...记 2m=n，那么（6.21）方程可以表达为更为一般的形式
加载中...时系统的运动.但是这样的运动能否在实际当中真正地实现呢？回答这个问题，就必须考虑（6.23）这个运动的稳定性.Ляпунов 给出这个稳定性的严格定义如下：
定义 任给一个 ε>0，不管它是如何地小，我们总可以找到一个相应的 η>0，使得，只要扰动引起初始状态和理想初始状态之间的偏差满足
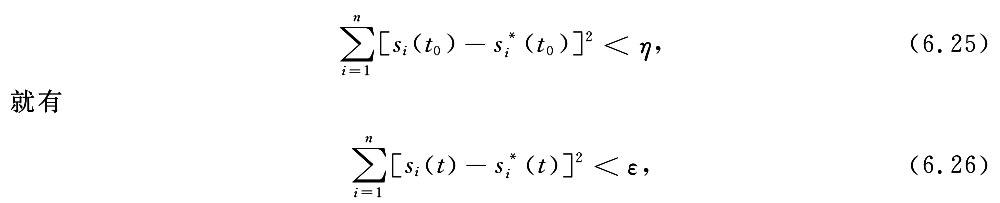加载中...其中 t≥t0.具有上述性质的运动（6.23），称为 Ляпунов 意义下稳定的运动；反之，称为 Ляпунов 意义下不稳定的运动.
我们称方程（6.22）的已知特解（6.23）为系统的未扰运动，而其他的运动 s（t）=［s1（t），s2（t），…，sn（t）］T为受扰运动.作受扰运动与未扰运动在同时刻的偏差
加载中...应该注意到，有
Xi（x1，…，xn，t）|x1=…=xn=0=0. （6.29）
这样，原系统的未扰运动就转化为以 x1，x2，…，xn为状态变量的系统的零解，而原系统未扰运动的稳定性（Ляпунов 意义下）也相应地转化为系统（6.28）的零解稳定性（同样在 Ляпунов 意义下），其定义为：
定义 任给 ε>0，不管它是如何地小，我们总可以找到一个相应的 η>0，使得，只要在初始时刻满足
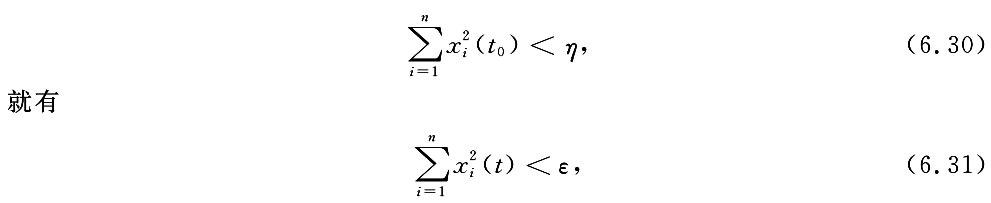加载中...其中 t≥t0.如果上述性质成立，方程（6.28）的零解称为 Ляпунов 意义下稳定的；反之，称为 Ляпунов 意义下不稳定的.
有时，还可以加强上述稳定性的要求.如果我们能够找到 η>0，使得只要在初始时刻满足
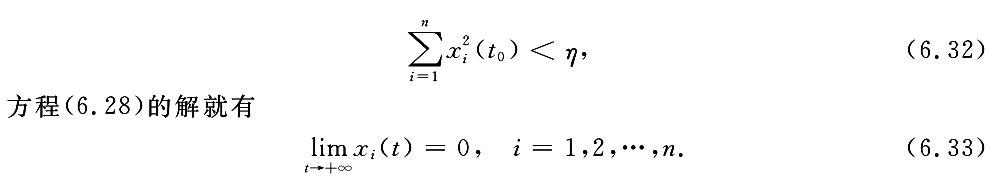加载中...这样，（6.28）系统的零解不仅是 Ляпунов 意义下稳定的，而且是渐近稳定的.
Ляпунов 意义下的稳定性概念并不是动力学研究中唯一的稳定性概念.由于 Ляпунов 稳定性要求受扰运动自初始时刻起，每时每刻都与同时刻的未扰运动相差很小（而且这个要求一直到 t→+∞ 都必须成立），在不少问题上，这种概念的要求是显得过于苛刻了.例如在天体轨道的研究中，一个天体运行轨道是否具有稳定性，我们只关心受扰运动的天体轨道是否在原轨道的邻近，并不要求这两个天体的同时刻偏差一定能受初始扰动的限制.举周期轨道族为例来说明.由于初始扰动引起轨道扰动，而轨道扰动往往同时有运行周期的变动.这样，即使很小的初始扰动，由于周期变动的缘故（虽然这个周期的变动是很小的），在运行时间足够长之后，两个轨道上的天体在同时刻的偏差也会增大到一定的数值.由此可见，Ляпунов 稳定性的要求对轨道稳定问题的研究来说是不适合的.Poincaré 在 Ляпунов 之前，早就提出了「轨道稳定性」的概念.它的定义可如下来叙述：
定义 设在状态空间里，某未扰运动的 s 轨迹为
s=s（t，α）， （6.34）
其中 α 为未扰运动的初始状态，即有
s（t，α）|t=t0=α， （6.35）
如果任给一个 ε>0，不管它是如何地小，总可以找到一个相应的 η>0，使得只要
加载中...对于任何的 t≥t0，总有 t′≥t0存在；反之，对任何的 t′≥t0，也存在 t≥t0，使下式成立
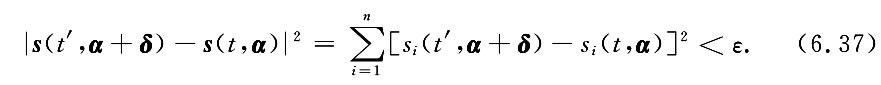加载中...这样，未扰运动 s（t，α）称为在状态空间里是 Poincaré 意义下轨道稳定的.
在某些情况下，轨道稳定性的概念也可以仅在位形空间里考虑.
Ляпунов 稳定性与 Poincaré 稳定性的要求是不同的.图 2.13 形象地对比了这两种稳定性概念的区别［17］.
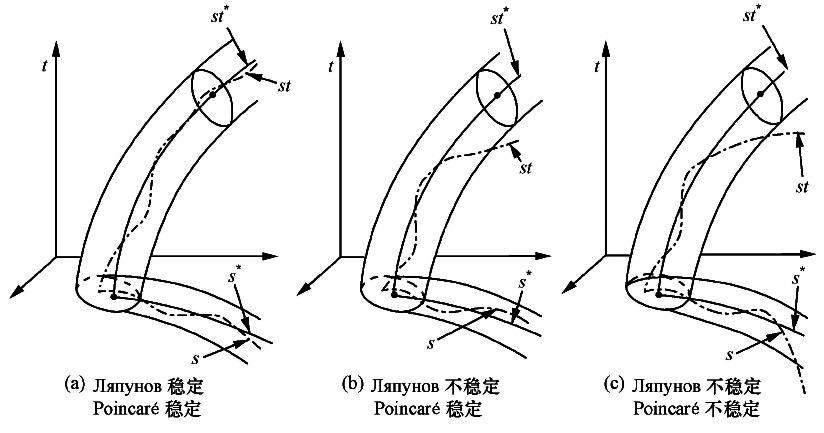加载中...图 2.13［22］
2.6.3 Ляпунов 函数与 Ляпунов 关于稳定性的定理
Ляпунов 在给出他的稳定性概念的同时，也发展了研究稳定性问题的直接法.这种直接法并不去寻求受扰运动微分方程的解，而在于去找出变数 x1，x2，…，xn，t 的某种函数，并使它关于时间 t 的全导数（求全导数时，认为 x1，x2，…，xn是满足受扰运动方程（6.28）的解）具有某些性质.通过这种定性的研究就可以判断（6.28）系统零解的稳定性.这种用以判断稳定性的函数我们概称为 Ляпунов 函数.很明显，这种方法是 2.6.1 小节中用能量函数 E 来判断稳定性的直接推广.