第二节 悬浮剂稳定性理论基础
第二节 悬浮剂稳定性理论基础
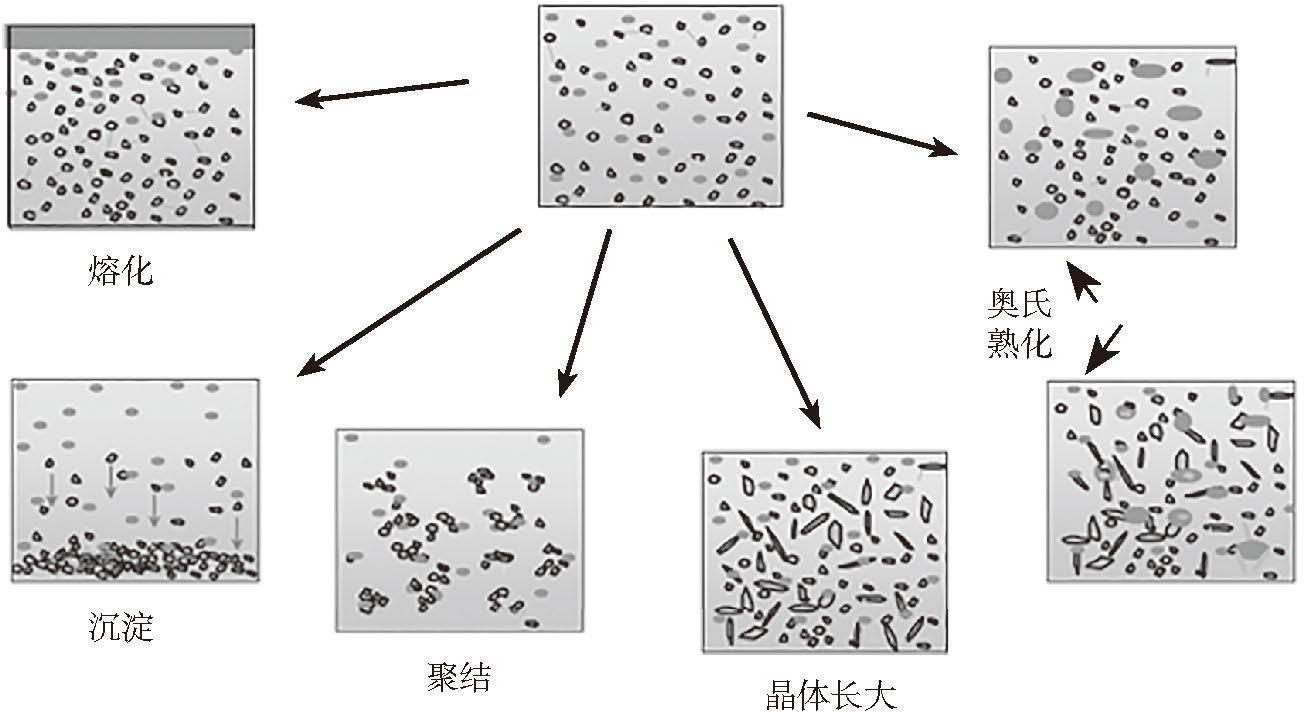
农药悬浮剂是介于液态和固态之间的一种剂型，属于多组分非均相粗分散体系。易受重力作用沉降分层，另外分散相颗粒比表面积大，具有较大界面能，有自动聚结的趋势，属于动力学和热力学不稳定体系。因此，悬浮剂在存放过程中易发生分层、絮凝、沉淀、晶体长大等现象（图 2-1），悬浮剂的稳定性，尤其是长期物理稳定性，一直以来都是一个相当棘手的问题。如何保持悬浮剂在贮存期间的稳定性，以及如何预测和评价农药悬浮体系的物理稳定性，是农药悬浮剂配方研究与加工中一个极为重要的问题，它既涉及基础研究，又涉及助剂的开发、加工工艺和设备的改进、检测技术和方法的建立、完善等。
加载中...
图 2-1 悬浮剂颗粒变化示意图
悬浮剂的稳定性理论研究涉及多个学科，目前尚不成熟。下面仅就悬浮剂稳定性的理论基础、悬浮剂稳定性的影响因子、悬浮剂稳定性的有效控制、悬浮剂长期物理稳定性的评估四个方面的相关研究进展做简单介绍。
一、悬浮剂稳定性理论基础
1. 悬浮颗粒间的沉降作用——Stokes 定律
农药悬浮剂中的分散颗粒粒径一般为 0.5～5μm，平均粒径为 2～3μm，属于粗分散体系。悬浮颗粒的相对密度一般大于液体，在重力场作用下，颗粒不断沉降，使得悬浮体系上下浓度不均一，破坏了其均匀性，从而引起扩散作用，下部的较浓颗粒向上移动，使体系的浓度趋于均匀。重力使悬浮颗粒沉降是悬浮体系的动力学不稳定性的重要表现。当两种作用力达到平衡状态时，各水平面的浓度保持不变，但从底部向上会形成浓度梯度。颗粒的沉降平衡需要一定时间，颗粒越小，所需要的时间越长。忽略分散的颗粒间的相互作用，假设分散粒子为球形，颗粒粒子的沉降速度基本上符合 Stokes 定律（2-1）：
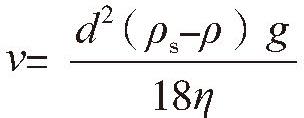加载中... （2-1）
式中 v ——粒子的沉降速度，cm/s；
ρs——粒子的密度，g/cm3；
ρ ——分散液的密度，g/cm3；
d ——粒子的直径，cm；
η ——分散液的黏度，mPa·s；
g ——重力加速度，cm/s2。
从 Stokes 公式可以看出，粒子的沉降速度v与粒子的直径d、粒子密度与悬浮液的密度差（ρs-ρ）成正比，与悬浮液的黏度η成反比。按照 Stokes 公式，悬浮液放置一段时间，颗粒都会沉降到容器的底部，上述是在假设条件下进行的，实际上颗粒还会受到温度变化、机械振动，特别是小粒子的扩散作用。在真实体系中，颗粒的沉降变得非常复杂，除粒径分布外，颗粒的形状、密度也多有差别，与均一球形偏离很远，悬浮体系的黏度和密度随沉降的发生而变化，颗粒与介质的相互作用，大颗粒的沉降对小颗粒的夹带等，都使沉降过程变得十分复杂。
2. 悬浮颗粒间的聚结作用——DLVO 理论
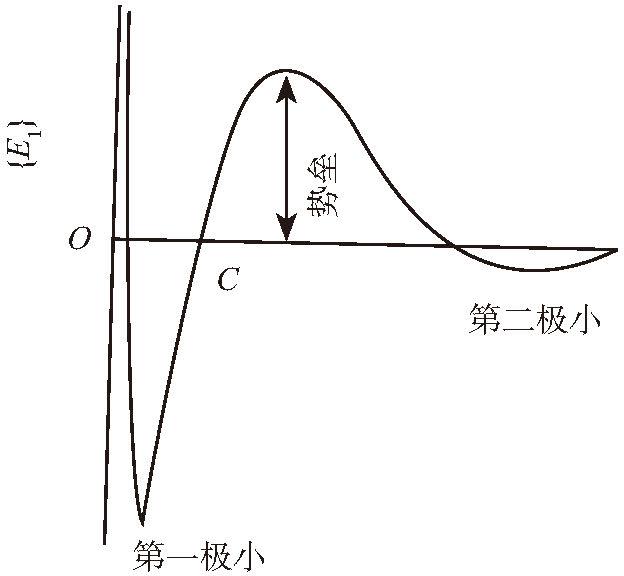
农药悬浮剂为高度分散的多相体系。由于悬浮剂中分散的颗粒很小，比表面积大，具有较大界面能，裸露的颗粒界面间亲和力很强，从而导致颗粒间聚结、合并变大。描述分散与团聚状态的经典理论是 20 世纪 40 年代苏联学者 Deryagin 和 Landau 与荷兰学者 Verwey 和 Overbeek 分别提出的关于各种形态微粒之间的相互作用能与双电层排斥能的计算方法，即 DLVO 理论（VT=VA+VR，VT为总势能；VA为范德华引力势能；VR为静电斥力势能）。一种胶体的所有稳定性都将取决于体系相互作用能量曲线的有效形式，即吸引能和排斥能两项之和与粒子分离距离的函数，见图 2-2。该理论认为颗粒的团聚与分散取决于颗粒间的 Vander Waals 作用能与双电层静电作用能的相对关系。当VA＞VR时，颗粒自发地互相接近，最终形成团聚；当VA＜VR时，颗粒互相排斥，形成分散状态。
加载中...
图 2-2 悬浮剂颗粒间能量曲线图
颗粒间的聚结与颗粒间的相互作用有关，将悬浮剂颗粒间的相互作用归结为范德华作用、「硬球」作用、双电层作用和位阻作用。范德华作用普遍存在于各种分散体系中，主要存在于极化和非极化的原子和分子间；「硬球」相互作用指中性稳定体系，在这种条件下颗粒是一个具有Rhs半径的硬球，Rhs半径稍大于实际半径，中心距离稍小于颗粒直径（2Rhs）时，会产生强烈的斥力，能量也随之增大；双电层作用存在于具有扩散双电层的静电稳定的颗粒之间，即低电荷体系中，人们通常用胶体稳定理论——DLVO 理论解释悬浮体系的稳定性作用；位阻作用存在于表面活性剂或接枝高分子物质的颗粒间，随着吸附层和接枝层相重叠时颗粒间出现的相互作用。
DLVO 理论是建立在分散剂完全覆盖于颗粒表面，吸附作用强，厚的吸附层，稳定部分处于良好的溶剂条件下的，对悬浮体系的研究具有一定指导意义，但 DLVO 理论不能解释高分子聚合物与非离子型表面活性剂的稳定作用，同时 DLVO 理论也忽略了静电斥力能以外的因素，但在很多情况下，实验结果和现象并不完全符合 DLVO 理论。
3. 空间稳定理论——HVO 理论
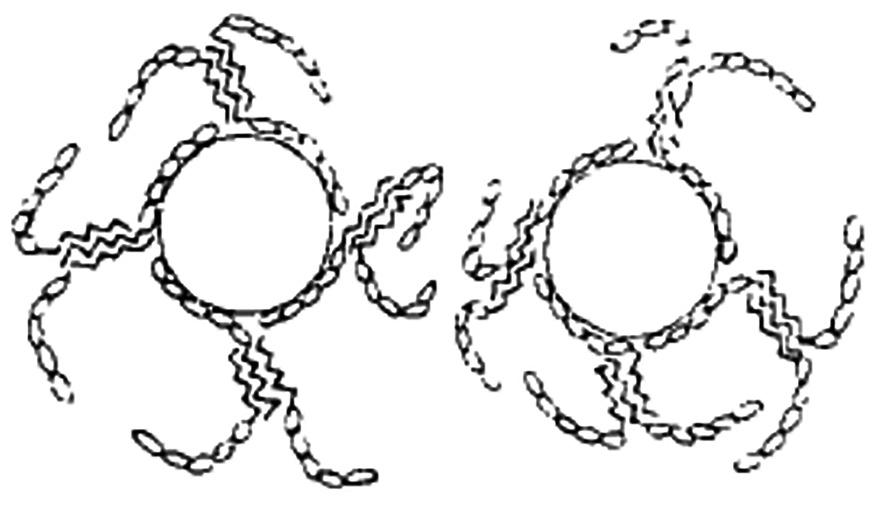
Hesselink、Vrij 和 Overbeek 等发现，在微粒分散体系中加入一定量高分子物质或缔合胶体时可显著提高悬浮液的稳定性，运用 DVLO 理论解释一些有高聚物或表面活性剂存在的体系稳定性，有时是行不通的。因为一个被 DVLO 理论忽略了的因素是聚合物吸附层的作用。在有聚合物存在的水溶液中，起稳定作用的主要是吸附的聚合物层而不是扩散层。空间位阻理论的解释是：聚合物的锚固基团吸附在固体颗粒表面，其溶剂化链在介质中充分伸展，形成位阻层，充当稳定部分，阻碍颗粒的碰撞聚集和重力沉降。高聚物或表面活性剂对固体颗粒表面性质的影响主要表现在以下三个方面：① 带电聚合物吸附的粒子表面会增加粒子之间的静电斥力，这一点同于 DLVO 理论解释。② 高聚物的存在通常会减少胶粒间 Hameken 常数，因而也就减少了范德华引力位能。③ 由聚合物的吸附而产生一种新的斥力性能-空间斥力位能，伸向溶剂的高分子链，使固体颗粒彼此之间相互排斥，提高悬浮液的稳定性，见图 2-3。
加载中...
图 2-3 空间稳定理论示意图
4. 空缺稳定理论
1975 年，B.Vincent 等首先发现自由聚合物对胶体的稳定作用，1980 年，澳大利亚的 Napper 提出与空间位阻效应不同的理论：非离子型聚合物在固体表面吸附很少，甚至是「负吸附」，只是以一定浓度分散在固体颗粒周围的分散介质中，即粒子表面的聚合物浓度低于周围的分散介质中的浓度，由这一「负吸附」现象而导致粒子表面形成一层「空缺层」，见图 2-4，当空缺层发生重叠时，就会产生斥力位能或吸力位能。在较低聚合物浓度的悬浮液中，空缺层的重叠会导致吸力位能占优，使体系聚沉；在较高聚合物浓度的悬浮液中，空缺层的重叠会导致斥力位能占优，使体系稳定。分散体系中分散剂（如表面活性剂及高分子物质）的重要作用就是防止分散质点接近到范德华力占优势的距离，使分散体系稳定而不至于絮凝或聚沉。分散剂的加入能产生静电斥力，降低范德华引力，有利于溶剂化，并形成一围绕质点的保护层。目前，空缺稳定理论还是一个新的胶体理论，还在逐步完善和发展。