免越獄超級簽過期提醒*電報加ctkj666.toh

CNN（卷积神经网络）是什么？有何入门简介或文章吗？

1410 赞同

71 评论

3360 收藏

本文是我关于机器学习的第一篇科普文，写了很久，希望能够通过仿生学、数学等角度，借助丰富的图片和动画帮助你直观了解CNN或者人工神经网络的原理。最后不能仅停留在理论，通过一辆跑车的实例将前面介绍的理论串联起来，了解CNN到底是如何运行的。话不多说，开始正文。

CNN全称是Convolutional Neural Network，中文又叫做卷积神经网络。在详细介绍之前，我觉得有必要先对神经网络做一个说明。

神经网络与仿生学

1. 仿生学

神经网络(Neural Network，NN)，我们又叫做人工神经网络（Artificial Neural Network，ANN），之所以叫人工，是为了和生物的神经网络做区分，因为人工神经网络其实是一种模仿生物中枢神经系统的数学模型或计算模型，由大量的人工神经元联结进行计算，用于对函数进行估计或近似。

人类很多技术的灵感都来自于仿生学。上帝创造了无数的生物，经过了亿万年的进化，都能够几近完美的适应周围的环境。而生物长期进化出来的能力对于人类的技术和生活又有很多的启示，人类很多科技发明的灵感都来自于生物。

比如

1. 翠鸟在水面捕食食物时，即使太阳光非常强烈，也能看到食物。我们知道，在水面反射光强烈，并且有波浪时，很难看清水下的景象。而翠鸟的眼睛有一种特殊的细胞，能够滤除太阳光中的蓝色光。后来，科学家仿照翠鸟的眼睛特点，制造了一台仿生学摄像机，观察同一片海域。普通摄像机只能看到蓝色的海浪，而仿生摄像机却能看到海中的海豚，座头鲸。

2. 蜘蛛丝是一种天然的纤维材料，在经过漫长的自然选择进化过程后，其强度和韧性之间达到了高度平衡，是人们垂涎上百年的特种材料。其织成的蜘蛛网可以轻易捕捉高速飞行的小虫，并且通常不会破裂，它既有磐石的坚固，又有蒲苇的柔韧。如果我们能廉价仿造，手腕粗的钢缆将被小指头粗细的蛋白质绳索取代，防弹服会像衬衣一样轻。所以蜘蛛侠中吐出的蜘蛛丝可以当绳索并承受人的重量是有理论依据的。

还有蝙蝠和雷达，鲨鱼皮游泳衣等。。。

可以说，大自然是人类的点子机器。那么，如果了解了人类大脑是如何思考的，是不是可以利用仿生技术，模拟大脑的思考过程，让计算机来完成人类大脑的思维过程呢？因为在计算机算法的发展过程中发现，有很多人类非常容易解决的问题，在计算机面前却是无能为力的，或者说错误率是非常高的，这就让科学家们想去探究人类的大脑是如何工作的。

比如人类很容易的能够识别下面的图片，左侧是数字4，右侧是一个苹果。但是在过去，对于计算机来说，想区分出数字或者各种水果是非常困难的。

于是这促使科学家研究人类的大脑是如何运作的，而由此发展出来的人工智能方向叫做人工神经网络，它的发展其实是依赖于生物科学，神经科学的发展，通过了解大脑的运作方式并将其仿生到计算机上，让计算机拥有人类大脑的思考能力。

既然是模仿生物神经系统，我们就需要首先了解一下生物神经系统的工作原理。如下图。

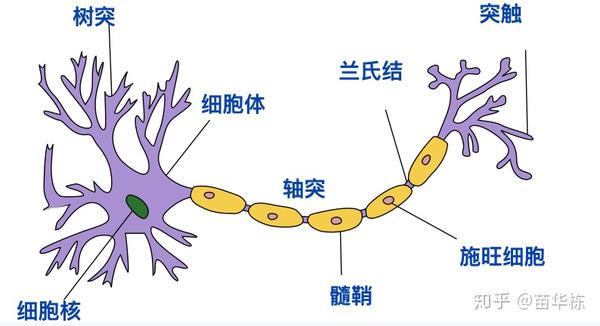
接收区（receptive zone）：树突到胞体的部分，会有电位的变化。树突接受不同来源的突触，接收的来源越多，对胞体膜电位的影响越大，反之亦然。而接受的讯息在胞体内整合。
触发区（trigger zone）：在胞体整合的电位，决定是否产生神经冲动的起始点。位于轴突和胞体交接的地方。
传导区（conducting zone）：为轴突的部分，当产生动作电位（action potential）时，传导区能遵守全有全无的定律（all or none）来传导神经冲动。
输出区（output zone）：神经冲动的目的就是要让神经末梢，突触的神经传递物质或电力释出，才能影响下一个接受的细胞（神经元、肌肉细胞或是腺体细胞），此称为突触传递。

而当很多个这样的神经元首尾相连，大脑就有了思考功能。

2. 人工神经网络

在我们设计人工神经网络时，其实就是在完全模仿生物神经网络的四个区，我们看一下人工神经网络中的神经元是什么样子的。

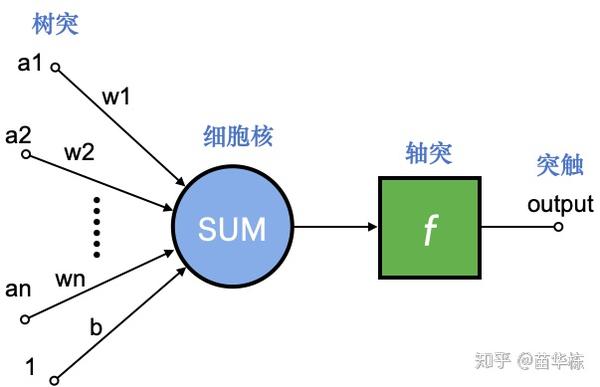
a1~an为输入向量的各个分量
w1~wn为神经元各个树突的权值
b为偏置(我们可以理解为权值，只不过输入为1)
f为传递函数，通常为非线性函数。
output为神经元输出

上图是人工神经网络中的一个神经元，其中我标出了对应生物神经网络相应的部位，相应的数学函数就是

$output = f(w_1a_1+w_2a_2+...+w_na_n+b)=f({{W^T}}{{A}}+b)$

为权向量，为的转置
为输入向量
为偏置
为传递函数

可见，一个神经元的功能其实就是求得输入向量与权向量的内积后，经一个非线性传递函数得到一个标量结果。多个神经元连接起来，就形成了类似大脑的神经网络。如下图。

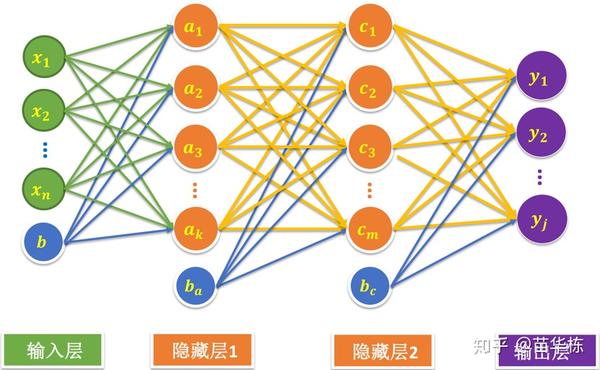
当然，人工神经网络是对大脑神经元进行了极简化抽象。在我看来，大脑的思考过程绝对不会是数学上的神经元简单的叠加，甚至神经元也不会是这么简单的抽象，应该是一个更复杂的系统工程。当然，这需要依赖于脑科学和生物技术的进一步发展，才能抽象出更接近人脑的神经网络。

不过即便我们对大脑神经元进行了这样的极简化，事实证明，它在工程上的效果也是非常不错的。

卷积神经网络

卷积神经网络（Convolutional Neural NetworkCNN）是一种神经网络，只不过在上面的神经网络结构中至少一层采用了一种称为卷积的数学运算，代替了传统人工神经网络的矩阵乘法 $f({{W^T}}{{A}}+b)$ 。卷积网络这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比，卷积神经网络在图像和语音识别方面能够给出更好的结果。

卷积神经网络除了最核心的卷积层以外，还包括线性整流层(Rectified Linear Units layerReLU Layer)，池化层（Pooling Layer）等，我们下面会一一介绍。

首先，在卷积神经网络中，卷积到底是一种什么样的运算呢？

1. 卷积层 ( Convolution Layer )

假设有一张5x5的图片，其中5的单位是像素(Pixel)，每一个像素其实是由RGB三种颜色通道组成，颜色范围是0 ~ 255，如下图。

为了简单起见，我单独抽出B这一通道来进行说明。

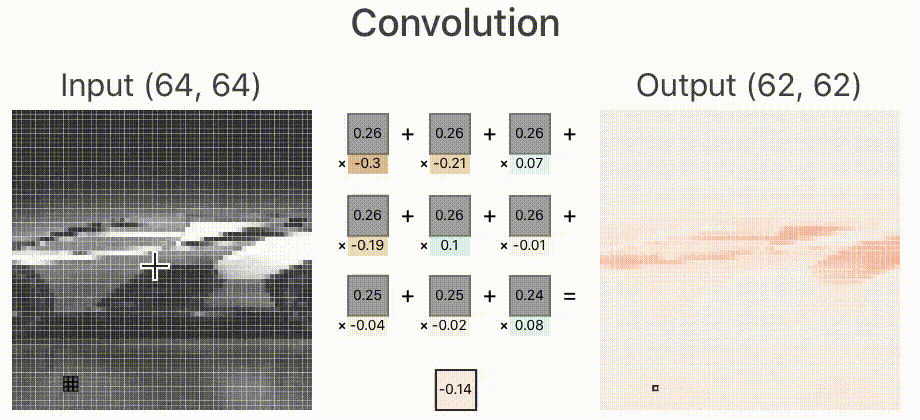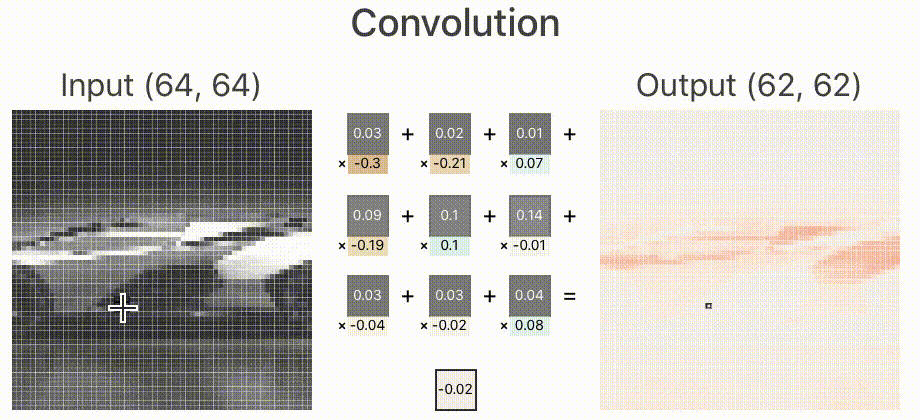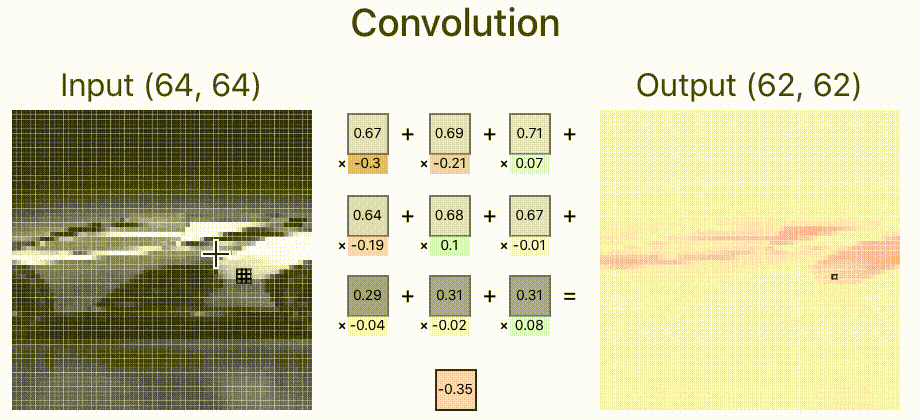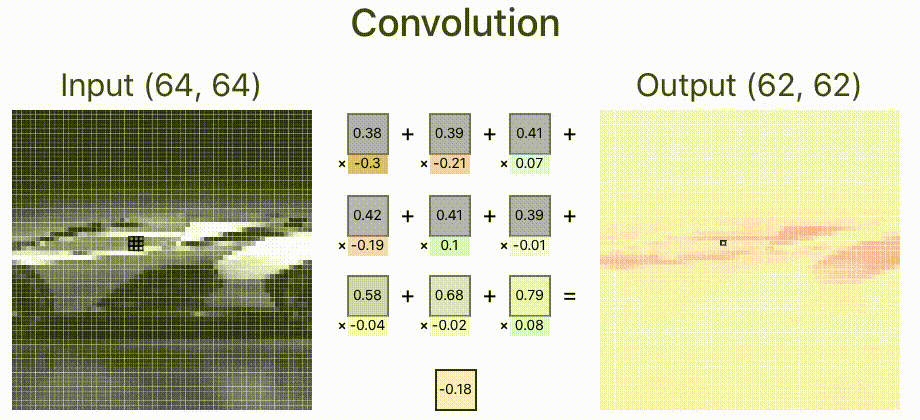
首先，卷积运算需要有一个卷积核，在图像处理中我们有时候又叫做算子，或者Filter。卷积核的结构一般可以看成是一个 $n\times n$ 的一个矩阵。比如我可以定义一个 $3 \times 3$ 的卷积核如下

$\begin{bmatrix}0 & 1 & 2 \\2 & 2 & 0 \\ 0 & 1 & 2 \end{bmatrix}$

我们让上面这个卷积核在图片蓝色通道上滑行，从左上角开始一行一行滑动，每次滑动步长为1，如下图所示。每一次滑动都会对应图片上的9个像素，让卷积核中的数字与图片中对应的像素值依次相乘，然后相加得到一个新数值，于是得到一个新的图片，如下图右侧绿色所示。

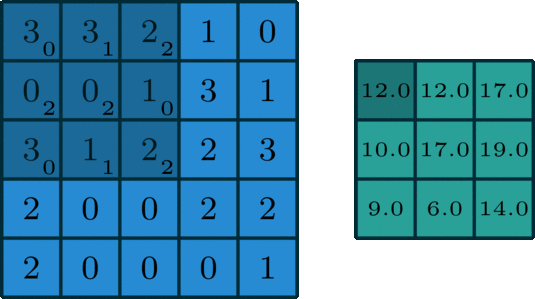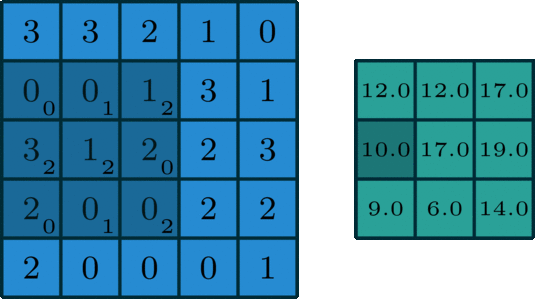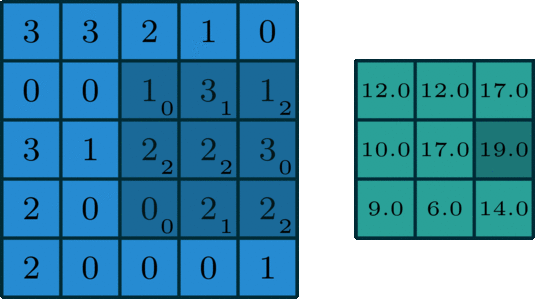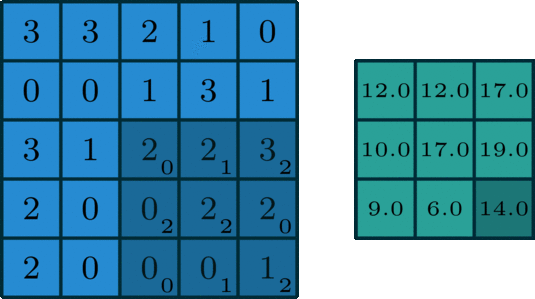
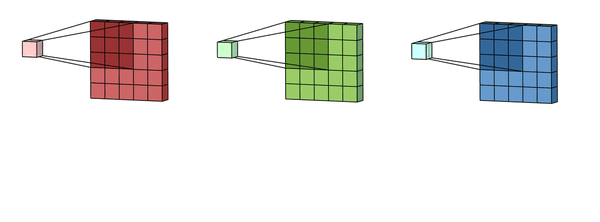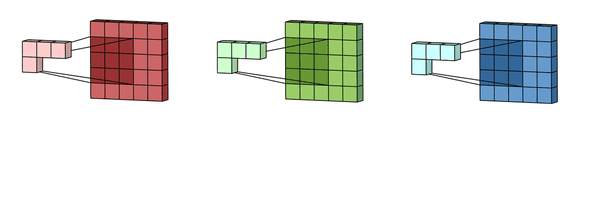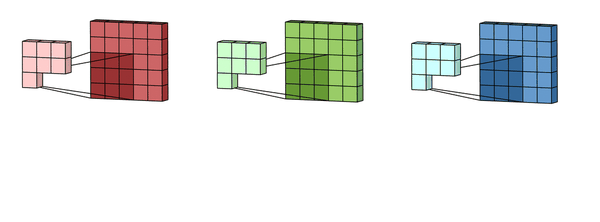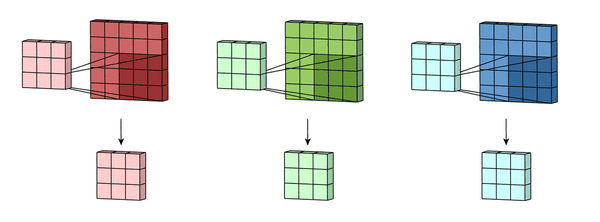
所以对于一个 $5\times 5$ 的图片，卷积核大小为 $3 \times 3$ ，滑动步长为1，则新生成的图片大小为 $3 \times 3$ 。更一般地，对于一个 $n \times n$ 的图片，卷积核大小为 $m \times m$ ，滑动步长为 1，则新生成的图片大小为 $(n-m+1)\times(n-m+1)$ 。

上面只对蓝色通道进行卷积，而一张图片有RGB一共3个通道，所以要对3个通道分别进行卷积运算，如下图所示。

上面提到的卷积其实只定义了一种纯数学运算，那么这种数学运算有什么直观的意义呢？卷积核和图片的像素相乘得到的新图片和原图片之间又有什么关系呢？我们来看一下下面几种特殊的卷积核效果。

=======================================

原始图片必须采用图像处理学术界的标准图像Lena，1972刊登在《花花公子》，如下图所示。

当然，作为福利，让大家看一下这位图像处理届女神在1997年的近照，依然风韵犹存。

=======================================

言归正传，挑选了几种常用的卷积核效果，如下图所示。

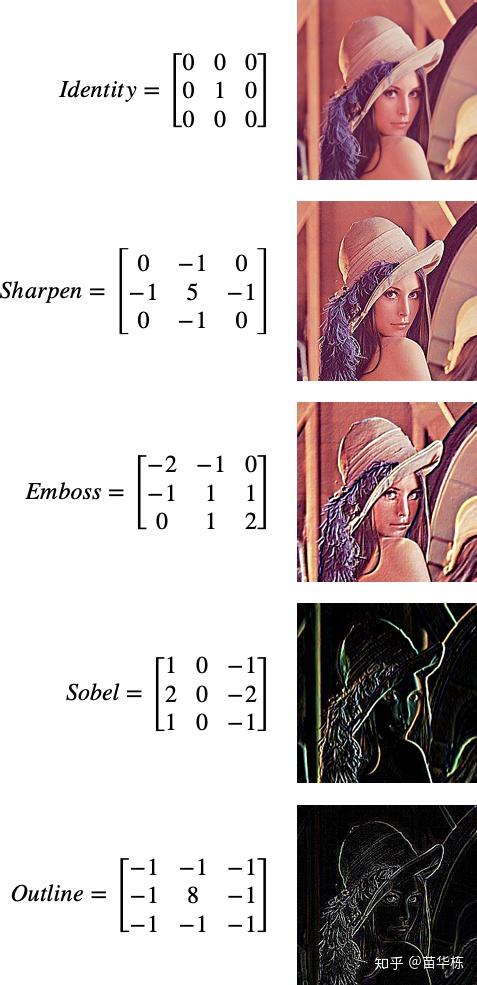
比如第一种卷积核Identity，只有中间的元素是1，所以其实没有对图像做任何改变，依然是原图形。

而对于最后一种卷积核，在图像边缘处（这里的边缘不是图片的四边，而是指像素突变的地方，比如Lena和背景的交界处就是边缘）像素会发生明显的变化，而在非边缘区（比如皮肤）像素的四周基本没有变化。所以用outline卷积核作用在非边缘区时，中间的像素和周围的八个像素卷积之后变为零，也就是黑色；而作用在边缘区时会呈现一个非零值。这样就提取了边缘信息。

中间的几个卷积核也是类似的原理。其实，Photoshop中的很多Filter都是基于上面的卷积核，比如Gauss Blur等，只不过卷积核的大小和对应的权值有区别，比如可能是 $5 \times 5$ 的卷积核。

所以，卷积核本质其实是对图片进行了Filter，不同的权值对应了不同的效果。当然，我们也可以把卷积核理解为对图片的特征提取。

比如最后一个outline，它提取了图片的轮廓，而弱化了图像中其它的像素。

再用Lena这张图片举例，如果要判定这张图片中是否是一个人，那么图片中人的特征是我们更关心的，比如这个图片中是否有头，眼睛，鼻子等主要特征，并且是按照人的五官的位置，比例进行排布。如果这些特征大部分都具备，我们可能会判断这个图片中是一个人。而当中的很多像素对我们来说都是无关紧要的，比如背景，比如肤色等等。

假如我建立了一个卷积神经网络用来对图像进行分类，用来判断图像是一辆跑车，还是一辆公交车，亦或是一杯卡布奇诺等等，如下图所示。第一步的卷积运算就帮我们完成图像特征提取的功能，忽略跟识别图像类别这个任务无关的像素。

那现在关键问题来了，卷积核中的权值应该如何取值才能完成针对图像分类这个任务的特征提取呢？

就像我们人类是如何识别出物体的呢？比如跑车和公交车，虽然非常类似，但是我们还是能够一眼分别出他们之间的差别，公交车更高更长更大一些，外形也没有跑车那么流线，车门的排布也不一样等。其实这个就是我们在进行分类时所使用的的特征提取。而这个特征是经过我们过往的学习经验而来的。

同样，卷积核的权值也是学习出来的，首先神经网络会输入大量带有标签的图片进行训练，其中的一组数据格式可能是（图片1，“跑车”）、（图片2，“船”），在输入大量的带有标签的数据训练时，我们会规定一个代价函数用来逐步调优卷积核的权值，保证权值对输入的样本数据能够尽可能的表现出较好的分类效果。

这样训练出来的权值就组成了一个个卷积核，至于为什么会是这样的权值，我们也不知道。这些权值更像是一个黑盒子，一旦训练出来，它只会按照数学上训练出来的最理想的特征进行提取，至于要完成什么特征提取可能就不会像上面那几个卷积核那么直观了。

上面说这些权值是学习出来的，这是因为神经网络是模仿人的大脑，那就必须具有人的基本智慧。我们在学校学习的时候，老师讲完例题后我们可以在不告诉答案的前提下，利用已经学习的知识和经验来解答课后练习题，这就是一种学习。

而这些卷积核的权值就和我们学习知识的过程是相似的，我们可能会输入10000张图片进行训练，具有学习能力的意思是训练出来的权值可以正确的区分它之前没有见过的图片。

专业一点的说法就是用训练样本对卷积神经网络进行训练，训练出来的参数对于测试样本依然具有良好的泛化性能，这才是一个表现性能良好的卷积神经网络。

2. 线性整流层 ( ReLU Layer )

和卷积层一样，名字听起来挺吓人，但其实非常的简单。从图像上看如下图所示

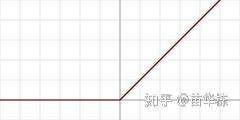
用数学表达式表示就是

f(x)=max(x0)

它其实就是我们前面提到的一种传递函数，我们又把它叫做一种激励函数或者激活函数(Activation Function)。

显然，ReLU是一种非线性函数，我们为什么不能使用线性函数作为传递函数呢？因为多层线性函数连接起来组成的神经网络和一层没有本质区别，因为再多的线性函数组合起来还是线性函数，只不过权值会发生变化而已，这样就失去了多层的意义。所以，在多层神经网络中，我们使用的传递函数一般都是非线性函数，这样连接起来才能起到多层的意义，才会有更好的学习能力。

其实有很多常用的激励函数，如下图所示。那么我们为什么要使用ReLU作为激励函数呢

从脑神经科学的角度来看，大脑神经元只有1%- 4%的部分同时处于激活状态，这是大脑在表现丰富性和能量消耗之间做的一个平衡，所以说大脑中神经元的激活其实是处于一种稀疏状态的。

(上面这句话来自 Paper《Deep Sparse Rectifier Neural Networks》，翻译出来实在是不太通顺，所以附上原文

Studies on brain energy expense suggest that neurons encode information in a sparse and distributed way (Attwell and Laughlin2001)estimating the percentage of neurons active at the same time to be between 1 and 4% (Lennie2003). This corresponds to a trade-off between richness of representation and small action potential energy expenditure.)

从ReLU图像中可以看出，在 $x \le 0$ 的范围内都处于非激活状态，只在 x > 0 时激活，这样保证了网络的稀疏性。而其它激活函数始终处于激活状态，只不过激活的程度不同，这与大脑神经元的工作方式不同。所以，从稀疏性的角度来说，ReLU更符合大脑神经元的工作原理。

当然，稀疏性还能够保证足够快的运算速度，其它激活函数无论激活强度多大，都得进行指数的运算，所以传递函数几乎无时无刻都在进行着运算，网络中几乎所有的神经元都在处于指数运算的工作状态，运行效率低下。而ReLU如果不激活，直接置零。即使激活，也是线性运算，速度非常快。

我们再看生物神经元激活的曲线，如下图。横轴是激活电流，纵轴是发射频率。发射频率我们可以简单理解为单位时间内的平均电峰数量，也就是细胞核对输入的触发响应。例如受神经驱动的肌肉的收缩力量，就单纯取决于动作神经元的“发射频率”，也就是单位时间内的平均电峰数量。

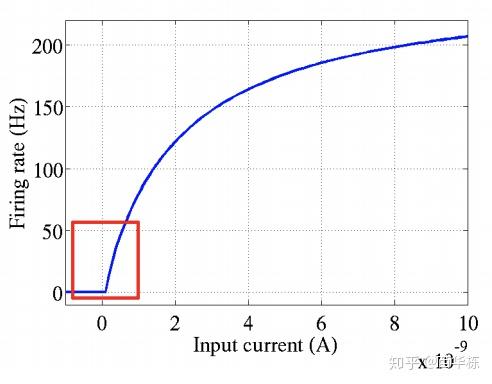
Common neural activation function motivated by biological data

我们可以看到，对于生物神经元刺激曲线，有如下几个特点

单侧抑制
广阔的兴奋区域

而这些特点都是ReLU所具备的，而前面介绍的两种其它的激活函数在两侧都有明显的抑制，与实际的生物神经元工作机理不同。

上面是从仿生学的角度来分析ReLU的实用性，当然从数学上来说，ReLU能够避免采用梯度下降时产生的梯度爆炸和梯度消失等问题，但这不是我在这里想要强调的。我觉得从仿生学的角度，更有利于让我们理解ReLU相比于其它激励函数的优越性。

事实上，即使如此简单的ReLU函数，在工程上的表现也是非常不错的，甚至超过Logistic Function和Tanh Function。

3. 池化层 ( Pooling Layer )

前面在介绍卷积层时，最后提到了一句话“用训练样本对卷积神经网络进行训练，训练出来的参数对于测试样本依然具有良好的泛化性能，这才是一个表现性能良好的卷积神经网络。”

这里泛化性能意思是我们在学习的时候不能学习过度，如果我们在学习人的图像时，学习到了人脸上的痣，皱纹，肤色等对于判定人来说无关紧要的要素，认为必须得具有痣或者是黄皮肤才是人的话，那么输入一个黑色人种可能就会被错误判定为不是人，我们就称这种现象叫做学习过度，专业术语叫做过拟合，也就是没有良好的泛化。

过拟合产生的原因可以这样理解，如果识别图像中的人需要50个特征，而我们在实际学习时，学习了100个特征，那么多的50个特征对我们来说就没有太大意义。即使这些特征在训练样本上可以很好的拟合，但是测试样本中可能没有这些特征，或者特征不明显，最后可能导致测试结果误差较大。如下图所示。

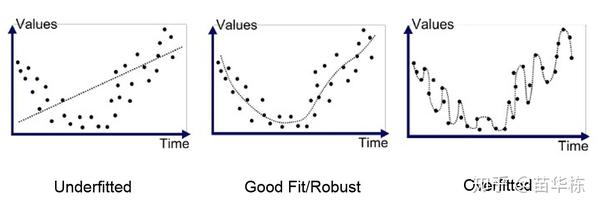
第一张图出现了欠拟合，因为实际的数据和输出结果相差很大。
第二张图泛化性能较好，因为输出结果反映了实际数据的整体趋势。
第三张图出现了过拟合，学习了过多的细节，虽然在训练样本中表现良好，但对于测试数据可能会出现较大偏差，不是我们所期望的效果。

所以，在实际的网络中，如果原始图像的特征较多，我们就需要限制特征的个数。限制特征个数最简单的办法就是降采样，在经过卷积层提取完特征以后，我们按照某种策略只提取图像中某个矩形范围内的一个像素。如下图所示，我们取 $2 \times 2$ 的矩形框，提取策略是像素最大值，于是经过降采样后就变为下图右侧所示，一个 $4 \times 4$ 的图像经过降采样以后变为 $2 \times 2$ ，大大减少了数据量。

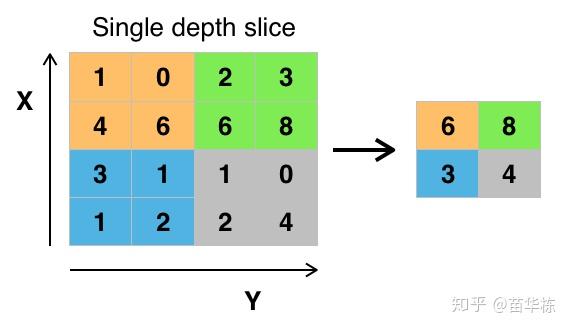
类似上述的降采样过程我们叫做池化，由于减少了像素，所以就忽略了部分特征，这样就减少了过拟合的现象的发生。

根据降采样策略不同，我们可分为最大池化(Max Pooling)，均值池化(Mean Pooling)等，上面的池化策略叫做最大池化。这也是在工程上表现较好的一种池化策略。

直觉上，这种机制能够有效地原因在于，一个特征的精确位置远不及它相对于其他特征的粗略位置重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。

通常来说，CNN的网络结构中的卷积层之间都会周期性地插入池化层。池化操作提供了另一种形式的平移不变性。因为卷积核是一种特征发现器，我们通过卷积层可以很容易地发现图像中的各种边缘。但是卷积层发现的特征往往过于精确，我们即使高速连拍拍摄一个物体，照片中的物体的边缘像素位置也不大可能完全一致，通过池化层我们可以降低卷积层对边缘的敏感性。

到此，卷积神经网络中核心的部件我们已经介绍完毕，包括卷积层，线性整流层，池化层三大组件。

实例

接下来我们一个实例来看一下CNN是如何运行的。假如我已经训练好了一个分类识别的卷积神经网络。如下图所示。

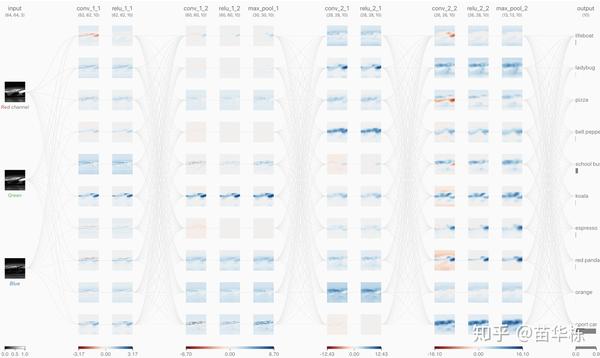
网络拓扑如下图所示

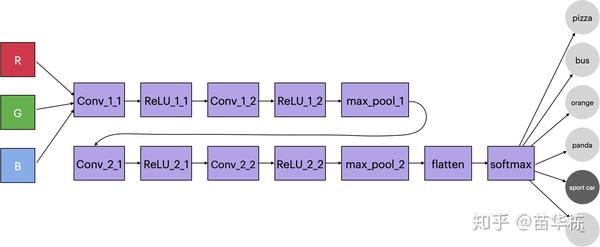
我输入下面这张兰博基尼Apis概念车的图片用来测试网络的输出。

当然，这个网络之前没有学习过这个车型，我们来看一下它是如何识别出这是一辆跑车的。

1. 首先，因为一个网络的输入大小必须是固定的，所以我需要需要将这张图片裁剪为指定大小，这里我转为 $64 \times 64$ ，卷积层中加入10个卷积核，分别用于提取不同的特征，卷积层是全连接的，卷积层的输出连接到ReLU层的输入。如下图所示。

这里的卷积层输入分别来自RGB三通道，其中RGB的范围是[0,1]，中间过程的输出我们用蓝色表示正值，红色表示负值，白色表示零。如果图片越红，表示值越小；越蓝，表示值越大。

下面的动图用来表示其中的一个卷积核计算的过程，分别对3个通道做卷积核，然后进行线性叠加。

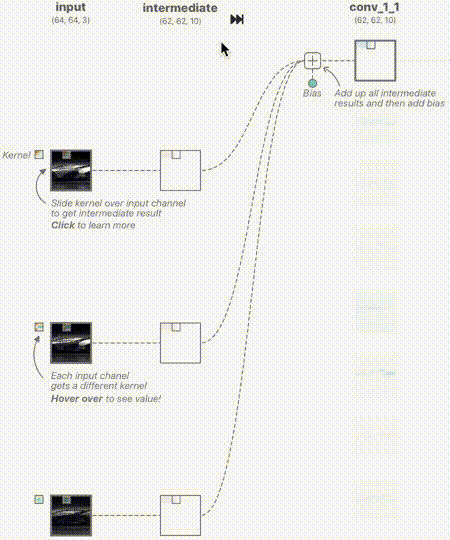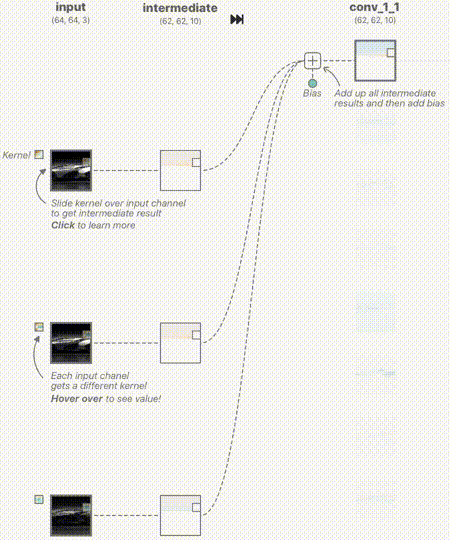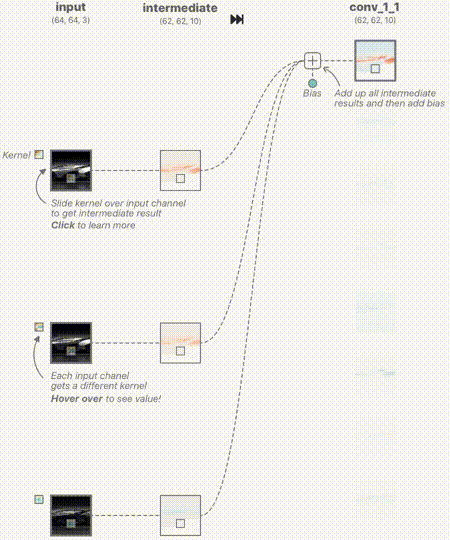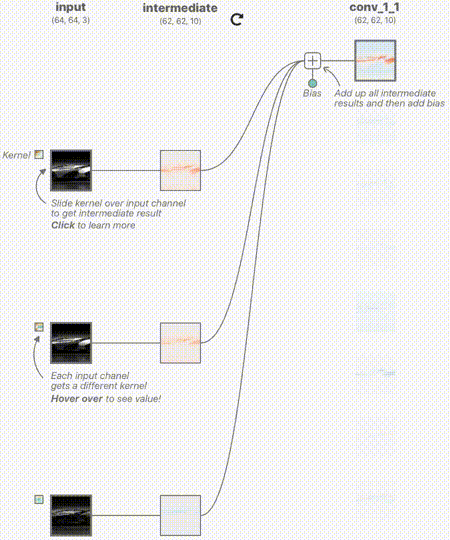
我们来深入看一下其中的一个通道的卷积核是如何工作的，如下图所示。其中卷积核的权值是训练出来的，至于需要提取什么特征，前面已经说过，它更像是一个黑盒子，一旦训练出来，单从权值上来看，我们无法直观的看出如何修改权值来提高网络的准确度。

2. 卷积层的输出即是ReLU层的输入。如下图，我们看一下ReLU层是如何工作的。

由于经过ReLU以后，所有的输出都变为正值，所以从图像上来看整体偏蓝。

3. 第一组卷积层和ReLU层之后，我们再次输入到一组新的卷积层和ReLU层，当然，新的卷积层中卷积核是不同的，只不过这一次我们要在最后降采样，所以在ReLU层后面加上一个最大池化层。

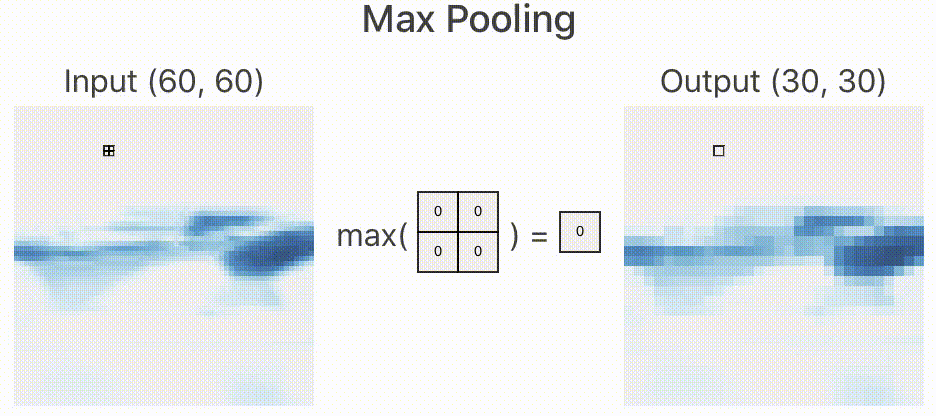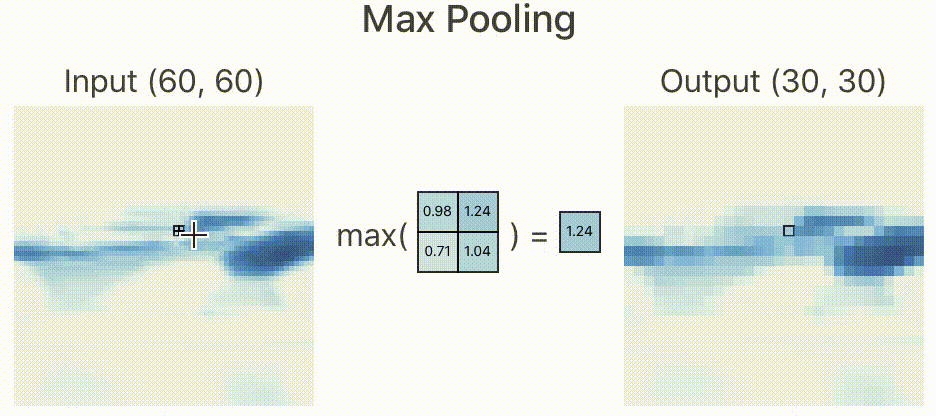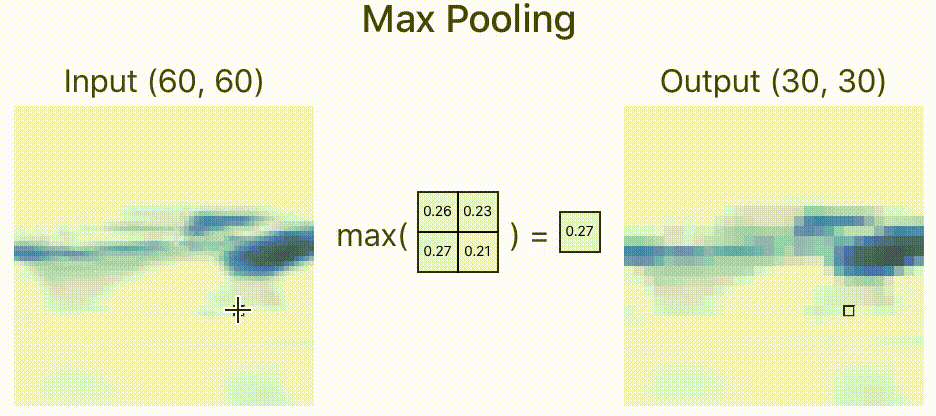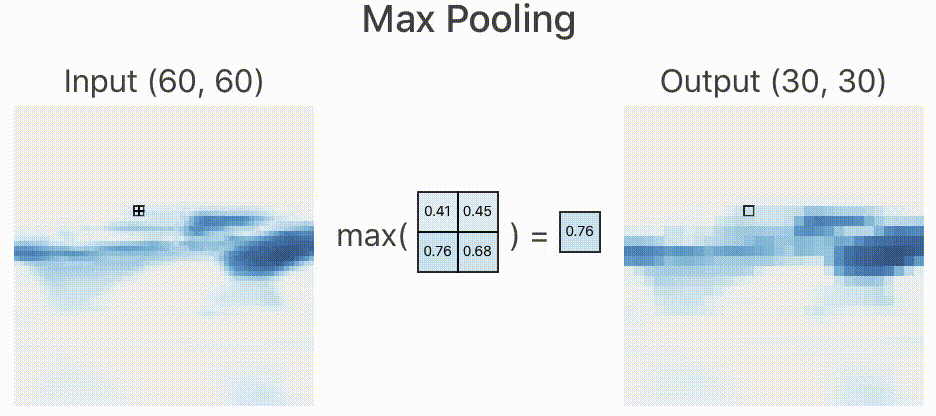
4. 到此为止，我们完成了下图所示的模块。

原始图像从 $64 \times 64$ 经过卷积层Conv11变为 $62 \times 62$ ，ReLU层不改变图像大小，又经过Conv_1_2变为 $60\times 60$ ，最后经过最大池化层变为 $30 \times 30$ ，图像减少了将近80%。

接下来，重复上面的这组模块，于是第二组最大池化层输出的图像大小变为 $13 \times 13$ ，到此图像大小减少了超过95%，可以说，我们已经抛弃了大部分无关紧要的特征。来看一下最后一步Max Pooling的图像是什么样子。

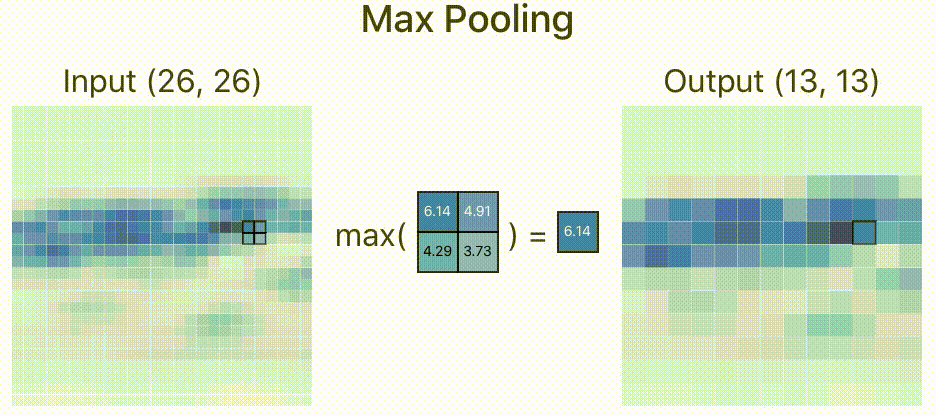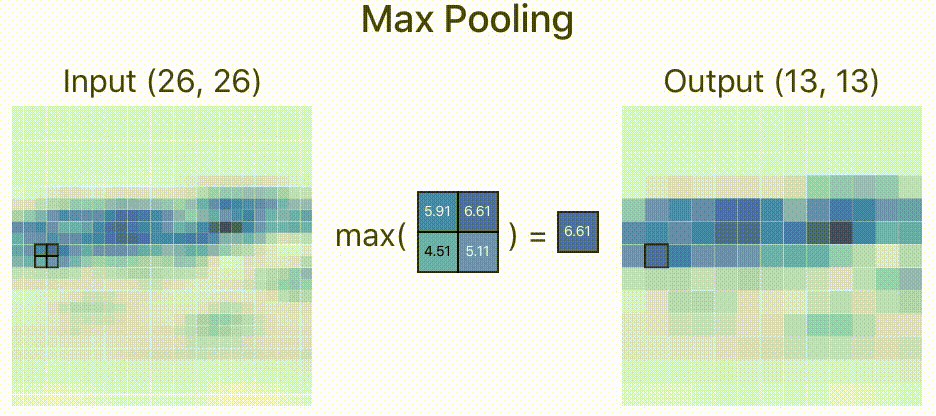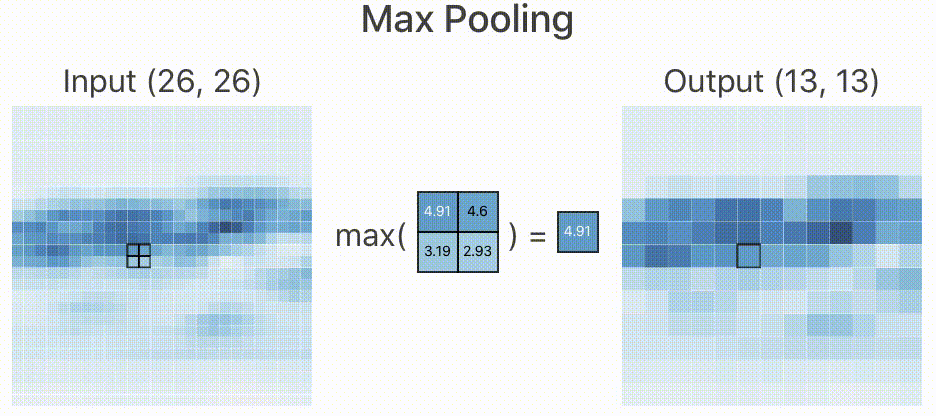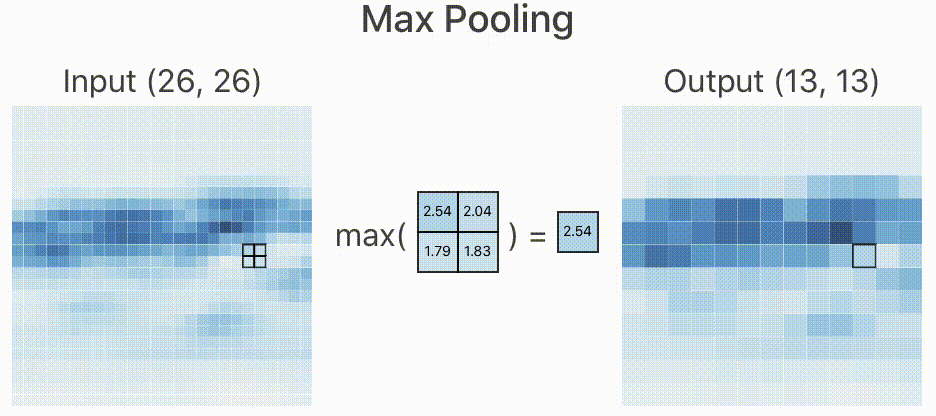
至少从我看来，当变为 $13 \times 13$ 以后，我已经看不出这是一辆跑车了。那既然人类都判断不出来，神经网络是怎么判断出来的呢？

别忘了，我们前面有10个卷积核，也就是卷积神经网络会提取10个不同特征，用来综合分析。仅靠上面这张图片的特征确实分辨不出来，但是10个不同的特征放在一起，咱们的卷积神经网络就能够分辨出来了。如下图所示，我们看一下在最后一步，这10个特征图都是什么样子。

这些特征我们从肉眼很难看到，因为这只是卷积神经网络通过训练的样本学习到的特征提取方式，这再一次证明了卷积神经网络中的权值就像是一个黑盒子。

5. 到此，我们的卷积神经网络的核心功能已经完成。但是输出还是二维的图像数据，我们需要将二维数据展平为一维数据，这个过程我们叫做Flatten，如下图所示。

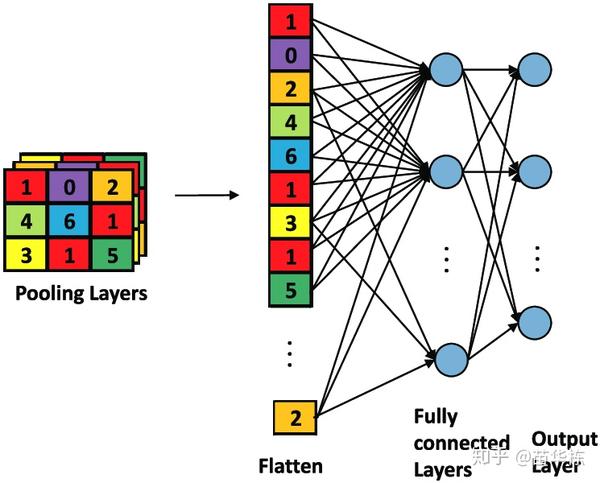
由于前面的图像大小是 $13 \times 13$ ，共有10个卷积核，所以Flatten后的数据大小是 $13\times 13 \times 10 = 1690$ 。

和前面介绍的人工神经网络类似，将展平后的一维数据与对应的权值做内积，只不过这一步的输入是1690维。

$output = f(w_1a_1+w_2a_2+...+w_na_n+b)=f({{W^T}}{{A}}+b)$

6. 前面Flatten层的输出经过和权值的内积之后，输入到全连接层(Fully Connected Layer)，全连接层的维数就是网络能够识别的图像类别数目，本例中是10个类别。

全连接层的下一层就是网络的输出层，输出层传递函数的输出结果就是这个网络最后的输出。我们期望的输出结果是图像属于某个分类的概率，所以如果某个输出结果的值比其他的大，就代表图像属于这个分类的概率要大于其他的类别。所以网络输出结果需要满足以下几个条件。

输出结果是概率形式，所以所有输出的范围都要归一化到
因为输出结果一定属于某个分类，所以所有输出结果的和是1

于是，这里我们就不能将Flatten和权值的内积直接输出，因为内积的结果可正可负，不是我们期望的范围。于是，最后一步我们经常会使用一种多分类函数softmax，又叫做归一化指数函数。它的数学表达式如下。

${\display \sigma (\mathbf {z} )_{j}={\frac {e^{z_{j}}}{\sum _{k=1}^{K}e^{z_{k}}}}} \quad for \ j = 1…K.$

我们看一下这个表达式是否满足上面提到的两个条件

$e^{z_{j}} > 0\ e^{z_{j}} < \sum _{k=1}^{K}e^{z_{k}}$ ，所以 ${\display \sigma (\mathbf {z} )_{j}={\frac {e^{z_{j}}}{\sum _{k=1}^{K}e^{z_{k}}}}} \quad \in (01)$ ，可以说这个条件比更加严格，满足条件1。
显然有 ${\display \sum _{k=1}^{K} \sigma (\mathbf {z} )_{j}= 1} \quad for \ j = 1…K$ ，满足条件2。

于是，网络的输出在经过softmax函数以后，就都变成 (01)范围内。

对于本实例来说，sport car的输出结果为

$\frac{e^{7.73}}{e^{3.95}+e^{2.72}+e^{1.19}+e^{-0.88}+e^{5.58}+e^{-9.95}+e^{3.75}+e^{-0.42}+e^{1.57}+e^{7.73}}=0.8551$

这个数值远远大于其它输出，所以判定结果是这张图片是跑车的概率要远远大于其它类别。到此，一个基于卷积神经网络的图像分类就完成了。

最后，十分感谢来自佐治亚理工的中国博士Zijie Wang将CNN可视化了，他的CNN Expainer能看到中间每一步的输出结果，甚至可以交互，是帮助大家理解CNN的利器，具体地址请参考参考资料。大家亲自体验一下应该会理解的更加透彻。

放在最后

近几年人工智能的发展非常迅速，自AlphaGo以来，人工智能在常人眼中更变得神乎其神，甚至认为人工智能无所不能。在这里，我们必须要认清人工智能的极限所在。

现代计算机的运行速度已经远超刚发明计算机时的速度，几亿倍不止。但是从计算机解决问题的角度来看，现代计算机和全世界正在设计的计算机都没有逃脱图灵机的范畴，可以说，图灵机为现代计算机和未来很长一段时间的计算都划定了一条不可逾越的边界，这个边界就是计算机处理问题的极限。这就如同热力学第二定律为热机效率划定了极限一样。

所以，当我们在思考人工智能的处理边界时，我们要明确以下几个事实。

世界上有很多问题，其中只有一小部分是数学问题。
在数学问题中，只有一小部分是有解的。
在有解的问题中，只有一部分是理想状态的图灵机能够解决的。
在后一类问题中，又只有一小部分是今天实际的计算机能够解决的。
而人工智能可以解决的问题，由只是计算机可以解决的问题中的一部分。

这个嵌套逻辑如下图所示。

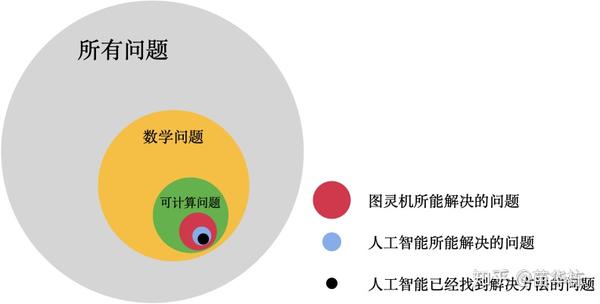
所以，人工智能所能解决的问题真的只是世界上问题很小的一部分。既然人们能够相信不能造出永动机，那么我们也应该相信人工智能在你有生之年是不可能超越图灵机的理论极限的。什么超人工智能，大家现在就暂当做科幻小说看一看就可以了。因为世界上还没有，而且也没有人在做非图灵机的计算机。

所以在解决和思考人工智能或者其他各类问题前，首先应该明确的是问题的极限，否则我们忙活了一顿，可能会发现自己只是在造永动机，而这将会是徒劳。

最后，如果你觉得这篇文章对你有帮助，请帮忙点赞，谢谢。

参考资料

Intuitively Understanding Convolutions for Deep Learning
Deep Sparse Rectifier Neural Networks
CNN Explainer
谷歌方法论. 吴军

编辑于 2023-02-10 · 著作权归作者所有